Матмодель вытеснения

В изучаемой математической модели, нефтяной пласт представлен суммой тонких слоев разной проницаемости. Плотность распределения проницаемости задано третьим распределением Пирсона,

$y(k)=a\cdot k^{b-1}\cdot e^{-ck}$

Плотность распределения, это отношение толщины слоя с заданной проницаемостью к общей толщине,

$y(k)=\frac{h(k)}{H}$

Функция распределения, это накопленный вклад толщин с проницаемостью от нуля до заданной, в общую толщину, нормированная к единице,

$Y(k)=\int_0^k y(k)dk$

Вид распределения задаётся средним значением проницаемости и квадратом вариации,

$b=\frac{1}{V^2}$

$c=\frac{b}{k_{cp}}$

$a=\frac{c^b}{\Gamma(b)}$

Определение функции распределения, позволяет построить слоистую модель с различным контрастом проницаемости по слоям,

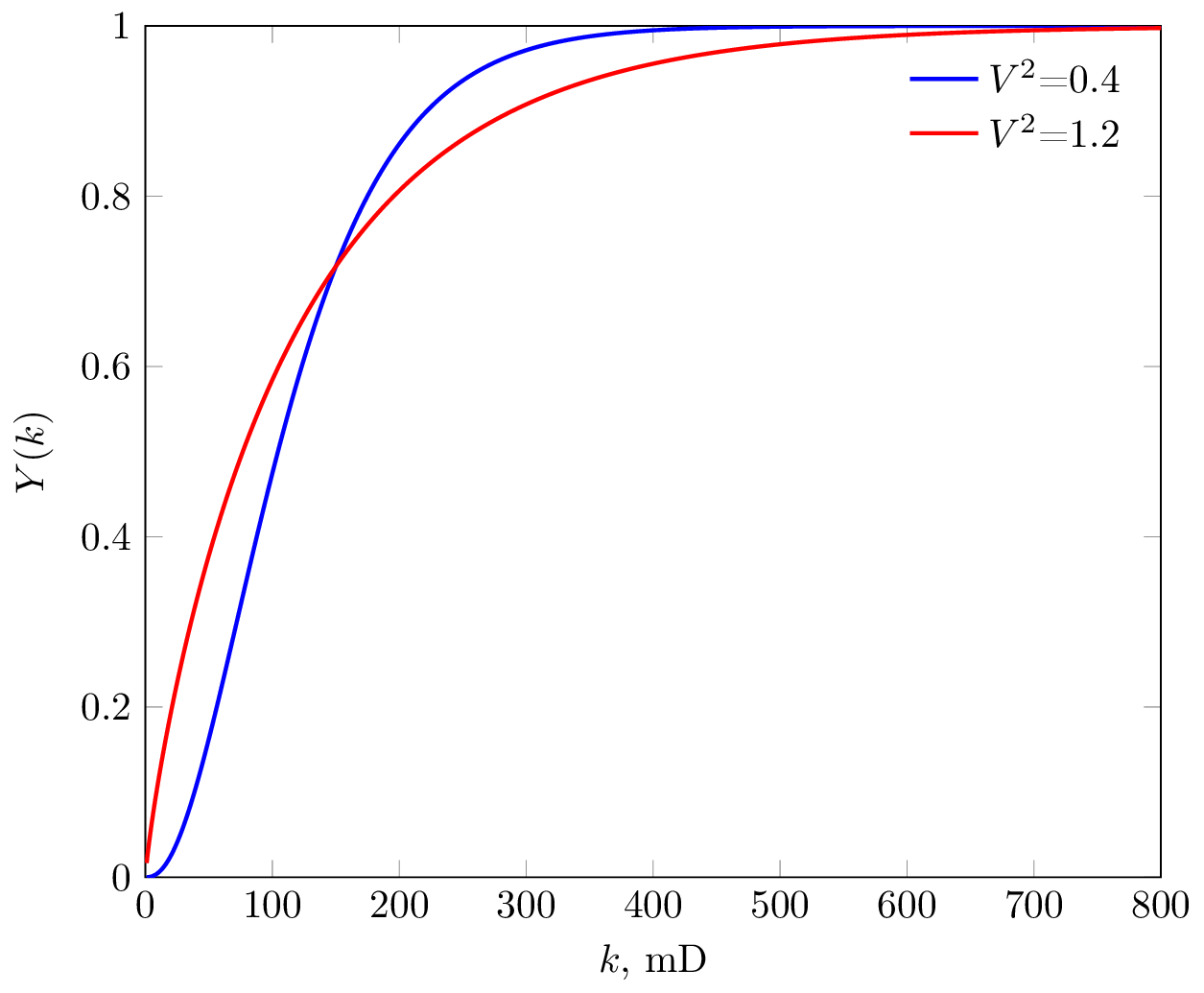
Начнем изучение процесса вытеснения нефти водой с самого простого случая, описание которого приведено в «Проектирование разработки нефтяных месторождений платформенного типа» (Э.Д.Мухарский, В.Д.Лысенко, 1973).

Нефть и вода имеют одинаковую подвижность, вытеснение происходит при линейном режиме фильтрации. Перепад давления в каждом слое остается постоянным со временем, следовательно скорость фильтрации и положение фронта вытеснения зависят только от проницаемости слоя.

В некоторый момент, после начала обводнения скважин, можно выделить граничный слой проницаемостью k^*, который делит общую нефтенасыщенную толшину на две части. Выше граничной толщины Y^*, завершено вытеснение нефти водой и пласт работает чистой водой. Ниже граничной толщины содержится остаточная нефть и всё ещё происходит процесс вытеснения нефти водой.

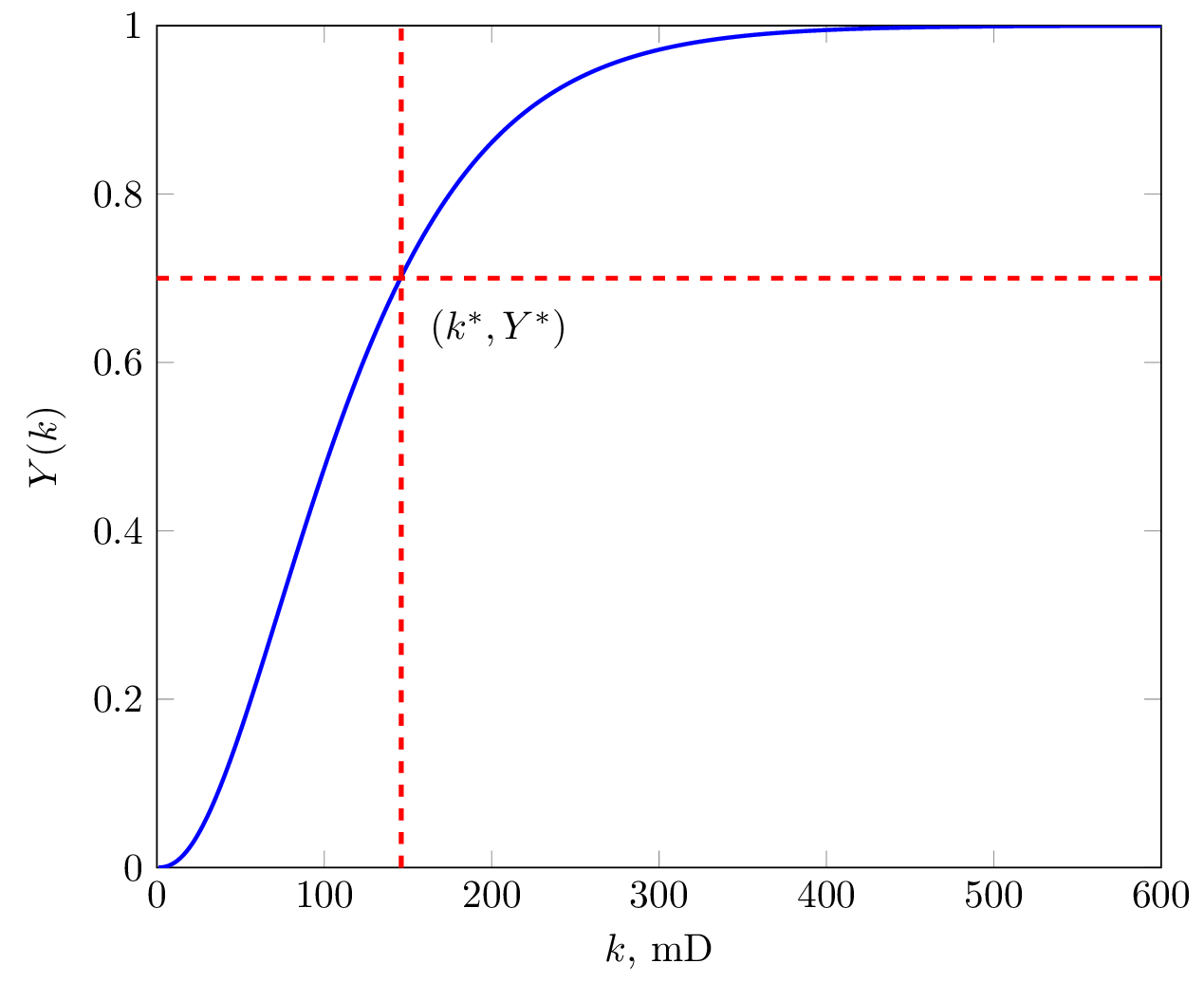
Положение фронта вытеснения для любого значения граничной проницаемости, можно получить растягивая форму распределения проницаемости от 0 до k^* в диапазон фиксированного расстояния от 0 до L.

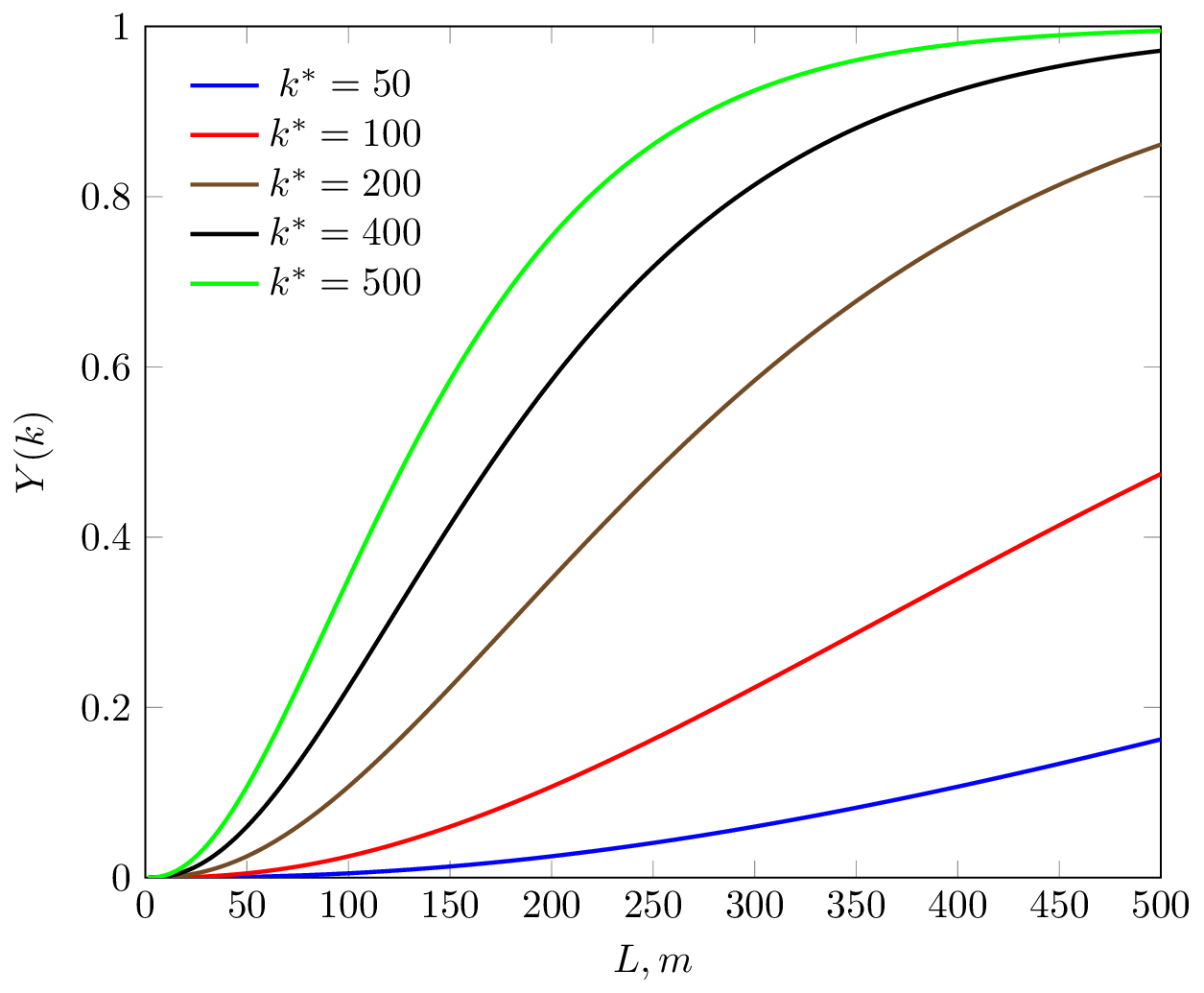
В области между нагнетательной и добывающей скважиной, выделим характерные регионы.

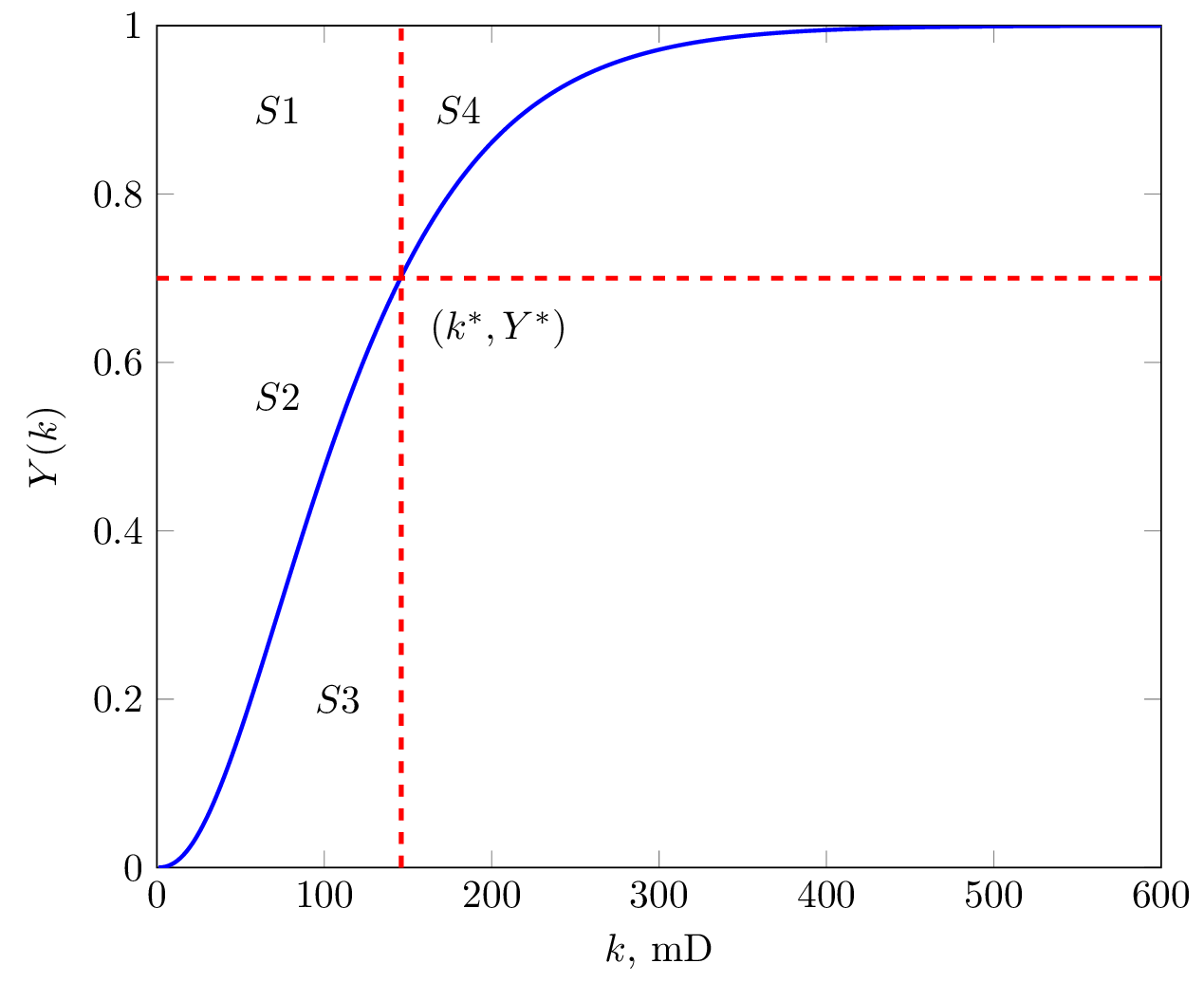
(S1+S2+S3) — объем пласта между нагнетательной и добывающей скважиной
(S1 + S2) — заводненная часть пласта
(S3) — часть пласта, содержащая оставшуюся подвижную нефть
(S4) — часть фронта вытеснения прошедшая за добывающую скважину, в случае если скважина не работала, или накопленный (суммарный) отбор воды скважиной

Далее выразим две замечательные характеристики, обводненность и отбор от извлекаемых запасов.

Обводненность W, можно найти из доли нефти в потоке

$1-W=\frac{S_2}{S_1+S_2+S_4}$

где,

$S_2=\int_0^{k^*} k \cdot y(k)dk$

$S_1+S_2+S_4=\int_0^{\infty} k \cdot y(k)dk$

следовательно,

$W=\frac{\Gamma(b+1,ck)}{\Gamma(b+1)}$

Отбор от извлекаемых запасов или коэффициент заводнения, определяется как отношение заводненной части пласта к общей площади пласта,

$k_z=\frac{S_1+S_2}{S_1+S_2+S_3}$

где

$S_1=(1-Y^*) \cdot k^*$

В итоге,

$k_z=1-Y(k^*)+\frac{b}{ck^*}\cdot(1-W)$

Изменяя значение граничной проницаемости, формируется характеристика вытеснения нефти водой для различных вариаций проницаемости,

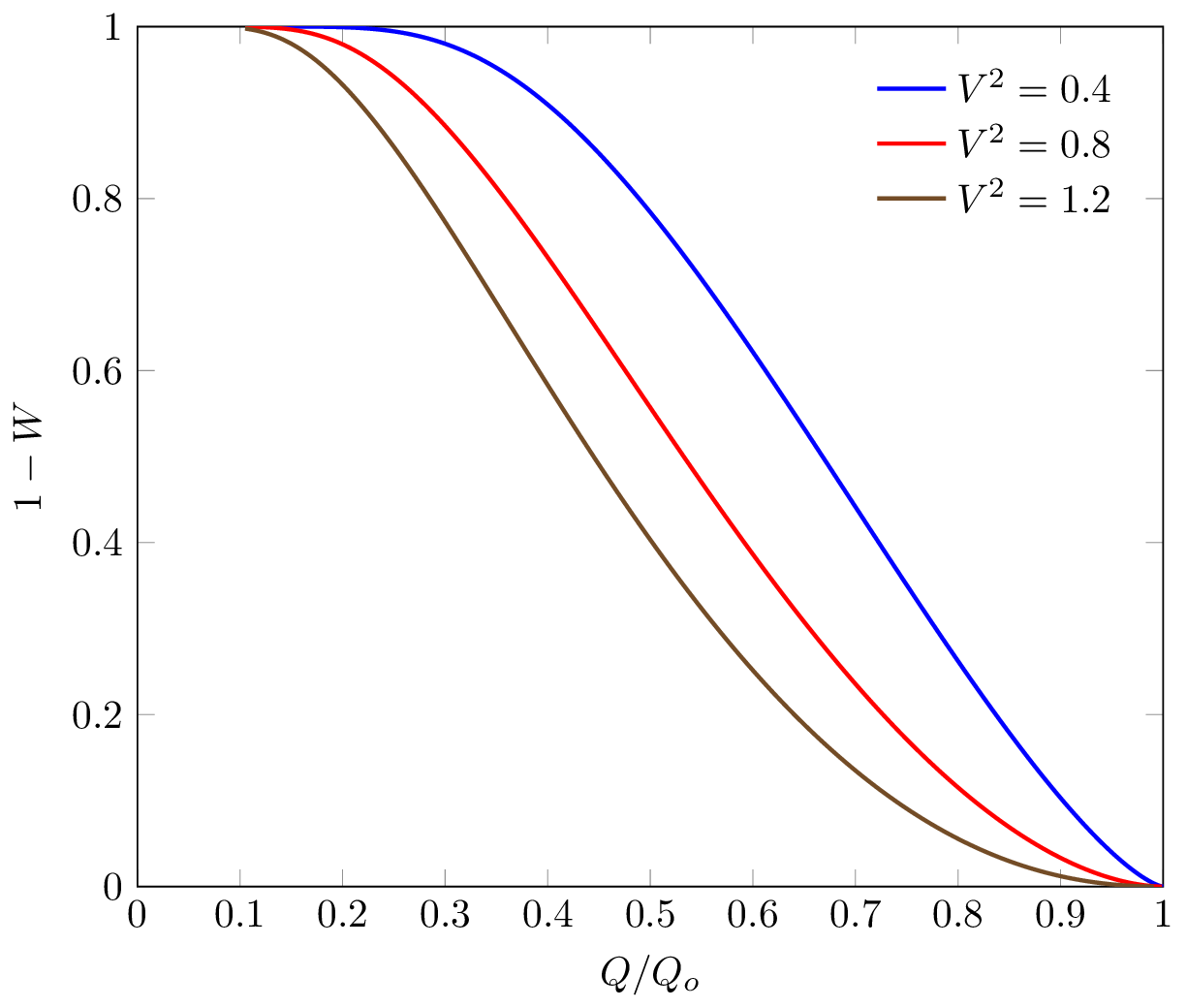
где коэффициент заводнения записан через отношение накопленной добычи нефти к извлекаемым запасам,

$k_z=\frac{Q}{Q_o}$

Далее перейдем к модели учитывающей различие в вязкости нефти и воды. Начнем с того, что запишем водонефтяной фактор,

$\frac{q_w}{q_o} = \int_{k*}^\infty \frac{k\cdot y(k) dk}{\mu_w} \Big / \int_0^{k*} \frac{k\cdot y(k)dk}{\mu_{o/w}}$

Параметр $\mu_{o/w}$ это вязкость водонефтяной смеси в одном слое, которая зависит от положения фронта вытеснения. Делая замену средним значением, неизвестное значение вязкости смеси можно вынести за знак интеграла,

$\frac{q_w}{q_o} = \frac{\mu_{o/w}^*}{\mu_w} \cdot \Big( \int_{k*}^\infty k\cdot y(k) dk \Big / \int_0^{k*} k\cdot y(k)dk \Big )$

Интегралы заменим соответствующими площадями,

$\frac{q_w}{q_o} = \frac{\mu_{o/w}^*}{\mu_w} \cdot \frac{S_1+S_4}{S_2}$

Отношение площадей можно найти из обводненности при равных подвижностях,

$1-W=1 \Big / \Big ( 1+\frac{S_1+S_4}{S_2} \Big )$

И окончательно,

$\frac{q_w}{q_o} = \frac{\mu_{o/w}^*}{\mu_w} \cdot \frac{W}{1-W}$

Повторив ход рассуждений для поверхностных условий и учитывая снижение фазовой проницаемости по воде при остаточной нефтенасыщенности, введем в формулу объемные коэффициенты нефти и воды и величину относительных фазовых проницаемостей,

$\frac{q_w}{q_o} = \frac{k_w \cdot b_o \cdot \mu_{o/w}^*}{k_o \cdot b_w \cdot \mu_w} \cdot \frac{W}{1-W}$

Далее заменяя всё одним коэффициентом различия физических свойств нефти и вытесняющего агента,

$\mu_D = \frac{k_w \cdot b_o \cdot \mu_{o/w}^*}{k_o \cdot b_w \cdot \mu_w}$

Получим компактное выражение для определения обводненности при различии свойств нефти и воды,

$w = \frac{\mu_D \cdot W}{\mu_D \cdot W + (1-W)}$

Таким образом, обводненность зависит от неоднородности проницаемости по слоям и различием физических свойств нефти и воды

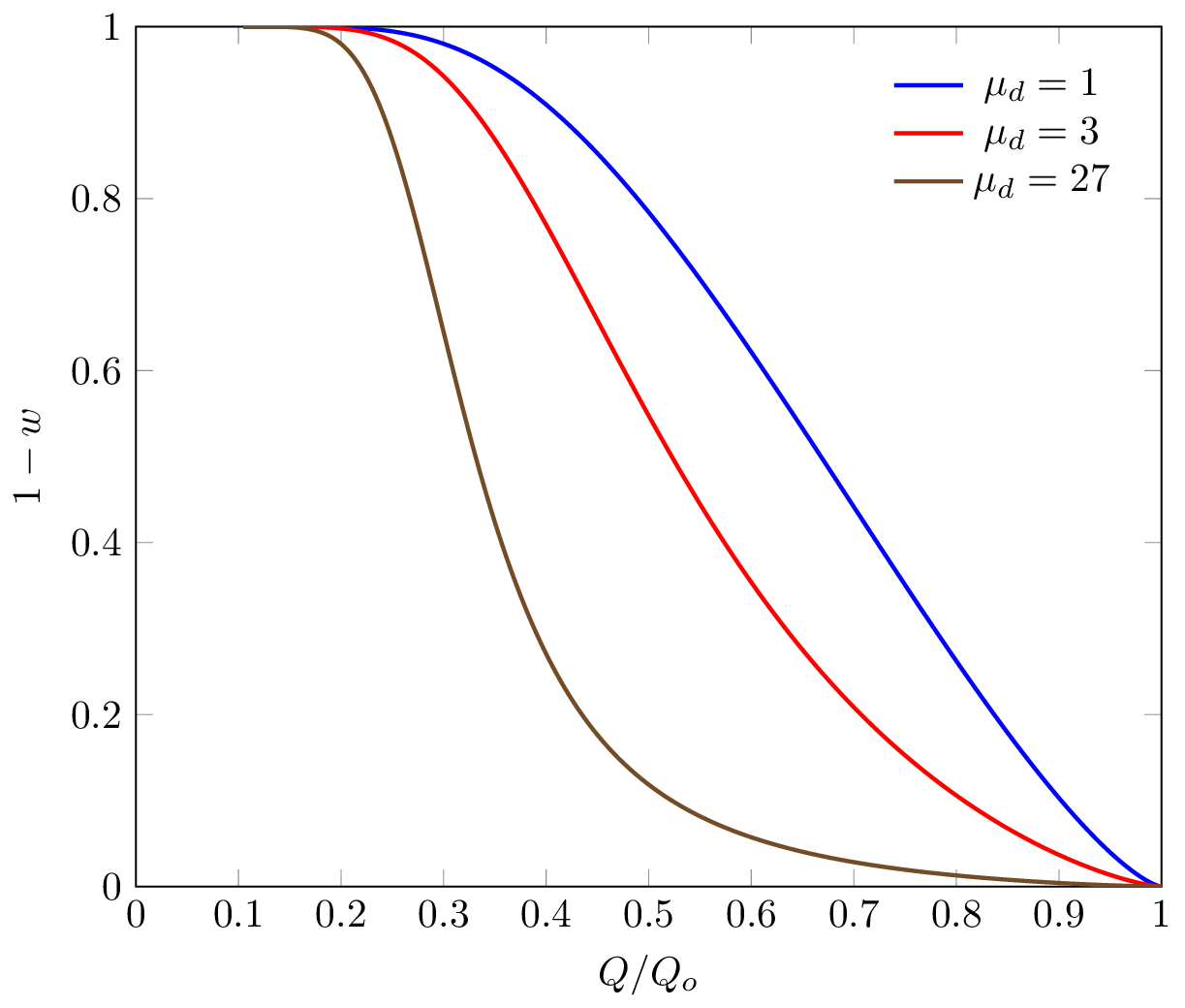
В оригинальном методе ТатНИПИнефть изучались разработка месторождения системой вертикальных скважин. Предполагалось, что в нефтенасыщенных слоях вязкость вблизи нагнетательных скважин быстро стремится к вязкости воды, а вязкость вблизи добывающих скважин остается зависимой от вязкости нефти, следовательно средняя вязкость это среднее значение между вязкостью нефти и воды

$\mu_{o/w}^*=\frac{\mu_o+\mu_w}{2}$

Коэффициент различия физических свойств определялся как,

$\mu_D = \frac{1}{2} \cdot \Big ( 1 + \frac{\mu_o}{\mu_w}\Big ) \cdot \frac{k_w \cdot b_o}{k_o \cdot b_w}$

В таком виде была придумана одна из частей универсального метода проектирования разработки нефтяных месторождений ТатНИПИнефть, описывающей динамику изменения обводненности элемента разработки, удивительным образом сочетающую простоту и полноту изучаемого явления.

Практическое моделирование

Добавить комментарий Отменить ответ

Комментарии

Архивы