Дебит горизонтальной скважины
В своей статье «Augmentation of Well Productivity With Slant and Horizontal Wells» (1988) Joshi S.D. представил самую известную наверное формулу для расчета дебита горизонтальной скважины и оставил в тексте статьи любопытную запись о том, что задолго до его работы в 1964 году Борисов Юрий Павлович сообщил о формуле расчета дебита нефтяной горизонтальной скважины, но к глубокому сожалению, Юрий Павлович вывода уравнения не привёл.
§1 Метод фильтрационных сопротивлений Борисова
В 1937 году Морис Маскет выпускает книгу «The Flow of Homogeneous Fluids Through Porous Media», в которой при рассмотрении интерференции бесконечного ряда добывающих скважин на некотором расстоянии от контура питания, приводит следующую формулу,
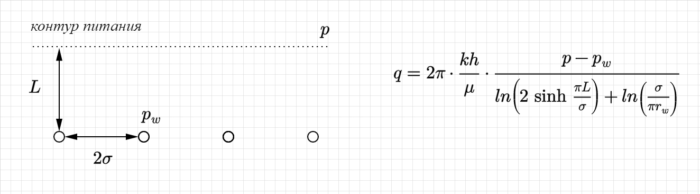
которую можно упростить, если расстояние до контура питания больше чем половина расстояния между скважинами
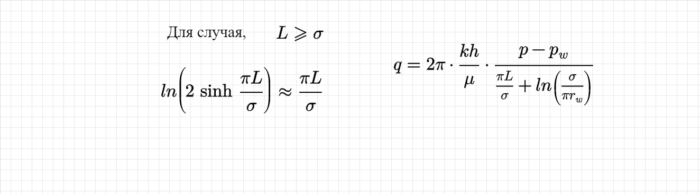
Юрий Павлович Борисов в статье «Определение дебита скважин при совместной работе нескольких рядов скважин» (1951) переписал формулу притока к цепочке скважин следующим образом,
![]()
где потери давления при линейной фильтрации жидкости, назвал внешним фильтрационным сопротивлением,
![]()
и потери давления в прискважинной зоне, внутренним фильтрационным сопротивлением,
![]()
Таким образом, совершив переход к электрогидродинамической аналогии закона Ома,
![]()
Для внутреннего радиального сопротивления, эквивалентный радиус контура питания определяется из равенства длины линейной галереи и длины окружности.
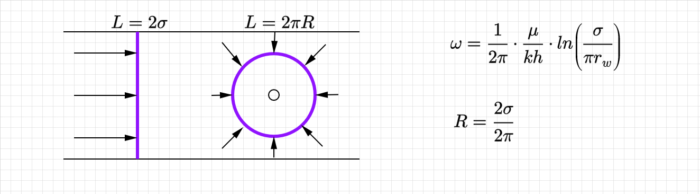
Борисов предположил, что и в более сложных условиях установившихся течений, фактические фильтрационные сопротивления можно разложить на внешние и внутренние фильтрационные сопротивления.
§2 Приближенная формула Борисова
Исаак Абрамович Чарный, вслед за Морисом Маскетом, издает книгу «Подземная гидромеханика» (1948), где повторяет вывод уравнения притока к бесконечной цепочке скважин, как утверждается более коротким способом и применяет способ вывода формулы к горизонтальной скважине.
В его представлении, горизонтальная скважина бесконечной длины располагалась в пласте толщиной ![]() на расстоянии
на расстоянии ![]() от линейного контура питания и дебит записывался следующим образом,
от линейного контура питания и дебит записывался следующим образом,
![]()
Особенность представления формулы при расчете дебита скважины конечной длины даёт значительную ошибку и пригодна только для полосовой залежи.
Ю.П. Борисов совместно с В.П.Табаковым в своей известной книге «Разработка нефтяных месторождений горизонтальными и многозабойными скважинами» (1964), приводит простую и удобную для расчета приближенную формулу, обладающую тем не менее вполне удовлетворительной точностью.
Фильтрационное сопротивление горизонтальной скважины, представляется суммой внешнего фильтрационное сопротивления от контура питания до вертикальной трещины, вскрывающей пласт на всю толщину и внутреннего фильтрационного сопротивления, представляя горизонтальный ствол как развернутую вертикальную скважину.
Внешнее фильтрационное сопротивление определяется по формуле притока от эллиптического контура питания к галерее, приведенную у Маскета (1937),
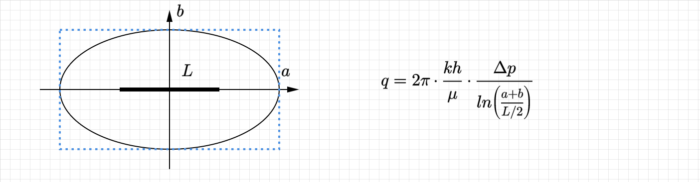
Маскет использует свойство фокусного расстояния эллипса, поэтому из трех величин ![]() требуется знать только две.
требуется знать только две.
![]()
Поэтому внешнее фильтрационное сопротивление запишется как,
![]()
Для относительно короткой горизонтальной скважины, форма контура питания не играет существенной роли и можно принять, что ![]()
![]()
Внутреннее сопротивление горизонтальной скважины записывается как,
![]()
![]()
Итоговая формула Борисова для определения дебита горизонтальной скважины,
![]()
Сравнение с известными результатами моделирования на электрической модели скважины и аналитической формулой Меркулова, показало отклонение упрощенной формулы Борисова не более 2%.
§3 Французский след
Через почти 30 лет после работ Борисова, в 1980 Французский Институт Нефти (IFP) переводит на французский язык книгу, получившей название «Exploitation des gisements de petrole par des puits orizontaux et a deviations multiples».
На основе изучения советского опыта, французский специалист F.M.Giger публикует большое количество статей, описывая метод Борисова и Меркулова,
«Reduction du nombre de puits par l`utilisation de forages horizontaux», 1983
«The Reservoir Engineering Aspects of Horizontal Drilling», 1984
«Horizontal Wells Production Techniques in Heterogeneous Resevoir» 1985
«Low-Permeability Reservoirs Development Using Horizontal Wells» 1987
Для ответа на вопрос, почему IFP заинтересовался советскими публикациями о расчете дебитов скважин, обратимся к истории развития горизонтального бурения.
После проведения в СССР успешных экспериментальных работ по бурению двух стволов длиной 30 и 35 метров в 1947 году, группа работников начала разрабатывать специальную технику и технологию бурения многозабойных горизонтальных скважин. Большой вклад в развитии был сделан Григоряном Александром Михайловичем. В 1953 году бурится скважина 66/45 на Карташовском месторождении. Скважина имела 10 стволов, три ствола пробурены горизонтально длиной от 60 до 168 метров.
К 1968 году завершена рекордная скважина длиной 2507 метров, имеющая горизонтальное окончание длиной 632 метра.
В 1979 году Французский Институт Нефти (IFP) и компания Elf Aquitaine (Total), запускает исследовательский проект «FORHOR, Horizontal Drilling to Improve Hydrocarbon Production» с целью пробурить на границе с Италией четыре горизонтальные скважины. Длительность проекта составляла пять лет. К проекту привлекается советский автор Григорян Александр Михайлович, который за обещание приглашения работать во Франции, бесплатно передает технологию французской стороне.
Судьба изобретателя сложилась неудачно.
На следующий год Александр Михайлович был уволен с работы директором ВНИИ буровой техники Вадецким Ю.В и через несколько лет в 1988 Григорян А.М. был вынужден эмигрировать в США.
А здесь во Франции, после успешного завершения проекта FORHOR, компания Total и IFP образуют сервисную компанию Horwell (доли участников проекта 50/50), через которую начинает продавать технологию горизонтального бурения по всему миру естественно присвоив себе авторство проекта.
§4 Передача эстафеты в США, ошибка Джоши
В 1984 году, по заказу Phillips Petroleum Co (сейчас ConocoPhillips, США) книга Борисова переводится на английский язык, редактором книги которой назначен господин Садананд Джоши, с замечания которого я и начал эту статью.
Ознакомившись с работами Борисова и французского специалиста, в 1988 году господин Джоши пытается повторить вывод формул (SPE-15375-PA), однако не может справится с выражением для внутреннего сопротивления.
Вот что он пишет,
«The equation used by these authors has an additional ![]() term in the denominator of the vertical-resistance term. Because these references do not include the derivation of their equation, it was not possible to invistigate the reasons for this difference.»
term in the denominator of the vertical-resistance term. Because these references do not include the derivation of their equation, it was not possible to invistigate the reasons for this difference.»
«Авторы для выражения внутреннего сопротивления используют число ![]() в знаменателе. По причине того, что в статьях не приведены выводы, мне невозможно установить причины такого различия».
в знаменателе. По причине того, что в статьях не приведены выводы, мне невозможно установить причины такого различия».
Появление такого замечания от редактора, который подготовил к печати перевод книги Борисова, где приводятся выводы о притоке нефти к многозабойным скважинам, к батарее наколонных скважин в однородном и слоистом пласте с притоком подошвенной воды, более чем удивительно.
Затем, господин Джоши недолго думая придумывает схему, которая бывает мелькает в статьях малоизвестных авторов,
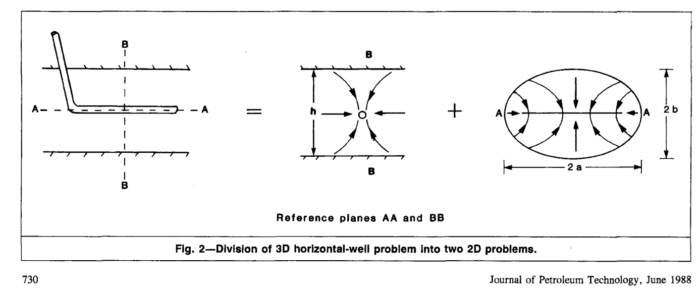
Из центральной схемы которого следует, что эквивалентный радиус радиальной фильтрации равен половине толщины пласта,
![]()
и переписывает уравнение для выражения внутреннего сопротивления в виде,
![]()
Тем самым незадачливый индус Садандад вносит ошибку в уже известные формулы расчета дебита горизонтальной скважины, породив уникальную формулу Джоши.
В августе 1992 года R.M.Butler из Университета Калгари, прекрасно знакомый со содержанием книги Борисова переведенной на французский язык в 1980 году, пишет официальное замечание господину Джоши, где указывает на его ошибку и объясняет почему в знаменателе появляется число ![]() .
.
На что господин Джоши достаточно резко отзывается,
«I do not agree with Butler`s comments. The equation that I presented in my paper will provide reliable horizontal-well-rate estimates for practical oilfield applications.»
Не соглашаясь с замечанием Батлера, упорный индус отрицает десятки статей и книг написанных задолго до его публикации в США пересказа формулы Борисова.
Моя формула хорошая, утверждает Садандад.
§5 Счастливое блуждание Экономидеса
Хорошей она оставалась до 1991 года, когда господин Экономидес публикует статью «Comprehensive Simulation of Horizontal-Well Performance» (SPE-20717-PA), где уже на гидродинамическом симуляторе изучает точность формулы Джоши и приходит к выводу, что формула обладает огромной ошибкой.
Для анализа использовалась формула Джоши (Борисова) с учетом анизотропии,
![]()
где коэффициент анизотропии, это отношение горизонтальной проницаемости к вертикальной и оказывает влияние только на внутреннее фильтрационное сопротивление,
![]()
Джоши указывает на необходимость соблюдать следующее условие,
![]()
иначе дебит вертикальной скважины становится больше дебита горизонтальной скважины.
Экономидес, продолжая традиции «научной школы США» начинает свою статью с повторения необходимости соблюдения условия и сразу же совершает подлог,
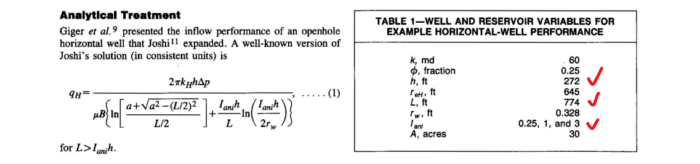
Исходя из таблицы исходных данных, для горизонтальной скважины L = 774 ft нельзя посчитать дебит при h = 272 ft и анизотропии = 3, ведь 272 * 3 = 816 больше 774 ft, в целом представленные исходные данные оторваны от вычислений в статье.
Далее приводится сравнительная таблица, в которой Экономидес представляет результаты расчета на гидродинамической модели с расчетами по формуле Джоши (Борисова).
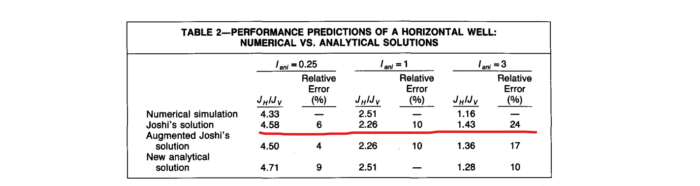
Экономидес для случая анизотропии 3, сообщает об 24% ошибке формулы Джоши и дает следующий комментарий.
«Efforts to improve the accuracy of the numerical solution (e.g. adding more vetical layers and diminishing the horizontal block size) showed that the numerical solution could not converge to Joshi`s formula. The condiferable difference, especially in highly anisotropic case, made it nessesary to invistigate the reason for these discrepanies.»
Далее сделан вывод, что для подавления ошибки в области высокой анизотропии, надо добавить в формулу Джоши следующий коэффициент,
![]()
Несложно убедится, что для анизотропии равной 3, Экономидес предлагает дополнить знаменатель числом (3 + 1) = 4, тем самым вернув на место потерянный коэффициент пи. Полученная формула получила название Джоши-Экономидеса и широко используется в технической литературе.
Тем не менее можно убедится, что формулы Экономидеса также не существует как самостоятельного объекта, это всего лишь исправление ошибки непонятливого индуса Садандада Джоши.
Ход истории заставил упорного индуса вернуть на место число Пи.
Здраствуйте уважаемый, Roman Kositsyn!
Не могу словами передать свой восторг от прочтения ваших статей….
Спасибо большое)
Я был бы счаствлив лично с Вами познакомиться с целью дружбы и обсуждения интересных вопросов нефтяной индустрии.
Роман, в приведённых классических работах анизотропия использовалась такая beta = (k.horizontal / k.vertical)^0.5, но вот попадались ли работы где вводится горизонтальная анизотропия aniz_horizontal = k.horizontal.max / k.horizontal.min? Ведь при снижении ФЕС aniz_horizontal начинает быть больше 1.0, а порой и существенно больше.
Анизотропия как отношение максимальной проницаемости к минимальной? Нет, не встречал. Думал будет вопрос, что под анизотропией бывает называют отношение permz/permx.
Вертикальная анизотропия — штука более менее понятная, а вот горизонтальная к сожалению не так сильно изучена, хотя она точно есть. Мы керн с Ачимовки тестировали, так вот выпилы с фазировкой 45 градусов на фильтрационных тестах хорошо так показали эллипсы по горизонтальной проницаемости.
Добрый день, Роман!
Написано очень увлекательно, прочитал с большим интересом. (В частности, очень признателен Вам за информацию о причине увольнения А.М. Григоряна в 1980 г, в других источниках я этого не нашёл.)
Но возникает следующий вопрос. В формуле Экономидеса член, отвечающий за внутреннее сопротивление, отличается от варианта в итоговой формуле Борисова не только добавлением (beta+1) в знаменателе под логарифмом, но также добавлением беты в числителе под логарифмом, а также добавлением беты в числителе перед логарифмом. Таким образом, под логарифмом вместо «примерного» 1/pi имеем отношение beta/(beta+1). Для рассмотренного Вами случая beta=3 это даст множитель 0,75 под логарифмом. И ещё тройку в числителе вне логарифма.
Не могли бы Вы, пожалуйста, пояснить, что здесь не так или что я неверно понял в статье.
Это я сократил получается изложение.
Там где указываю,
«Для анализа использовалась формула Джоши (Борисова) с учетом анизотропии»
приводится та же формула Борисова, только с учетом анизтропии. Я поместил число «пи» в квадратные скобки, чтобы сохранить запись Борисова. Без числа «пи» это формула которая анализировалась Экономидесом, её можно увидеть на скриншоте после слов
«Экономидес, продолжая традиции «научной школы США» начинает свою статью с повторения необходимости соблюдения условия и сразу же совершает подлог».
Я подумаю и перепишу это место, спасибо.