1. Скорость фильтрации, зависит от перепада давления на единицу длины,

\displaystyle v=\frac{k}{\mu}\cdot \frac{dp}{dl}

Проницаемость k отвечает за потери давления при фильтрации жидкости сквозь породу.

2. Дебит, это объем жидкости полученный за определенное время,

\displaystyle q = \frac{V}{t}

3. Дебит можно определить также из трубной гидравлики, умножая скорость движения частиц на площадь поперечного сечения,

\displaystyle q = v \cdot \omega

где под площадью сечения принято понимать геометрическую площадь, расположенную перпендикулярно потоку.

4. Однако в породе жидкость фильтруется сквозь поры, суммарная площадь которых в сечении всегда будет меньше геометрической площади. Поэтому вычисленная скорость фильтрации v это не настоящая скорости фильтрации жидкости.

5. «Введение понятия условной скорости фильтрации, позволяет рассматривать пласт как непрерывное поле скоростей фильтрации и давлений. Располагая данными о скорости фильтрации v и площади поперечного сечения ω легко найти дебит жидкости или газа, не вдаваясь в рассмотрение микрокартины движения жидкости или газов в резко изменяющихся по форме поровых каналах» («Подземная гидравлика», Щелкачев, 1949).

6. Тем не менее, условная «скорость фильтрации» используется для определения коэффициента проницаемости,

\displaystyle k= v \cdot \mu \cdot \frac{dl}{dp}

7. При рассмотрении установившегося режима фильтрации, положение линий изобар во времени остается постоянным. Частица жидкости движется от одной линии изобары к другой. Прослеживая траекторию жидкости в равные отрезки времени, область фильтрации можно поделить на равные объемы,

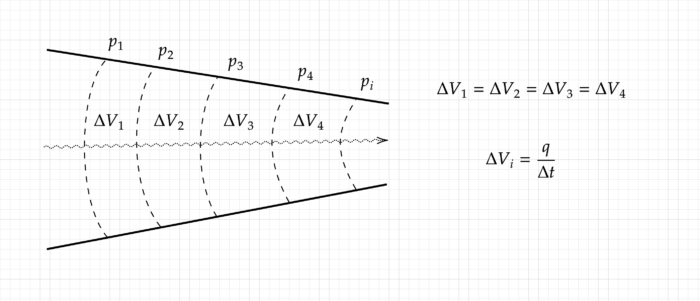
8. Так можно понять как происходит фильтрация.

Постоянный объем частиц поступает из-за контура питания. Через равные отрезки времени, пачки жидкости постоянного объема приближаются к забою добывающей скважины и в итоге извлекается на поверхность. Так как пачки объемов движутся без разрыва, объем добываемый скважиной равен объему пачки который в этот же момент поступает в область питания скважины.

9. Форма, которую занимает в пласте объем жидкости и потери давления зависит от типа фильтрации.

Для прямолинейного течения в пласте, потери давления i остаются постоянными при фильтрации сквозь каждый метр породы,

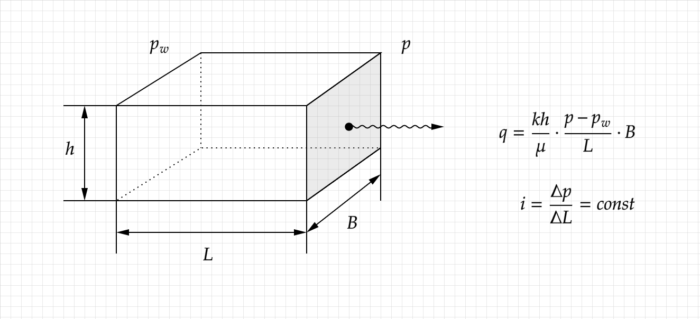
Для радиального течения потери давления уменьшаются при удалении от скважины, поэтому на дебит скважины имеет огромное влияние первые несколько метров фильтрации и почти не влияет расстояние и форма контура питания,

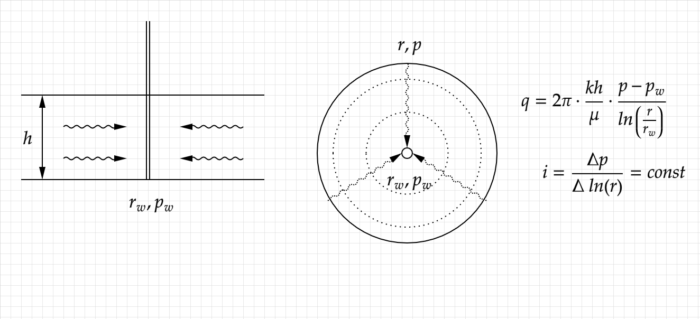
Сферическое течение в пласте встречается достаточно редко, потери давления сосредоточены на стволе скважины и дебит почти не зависит от радиуса до контура питания,

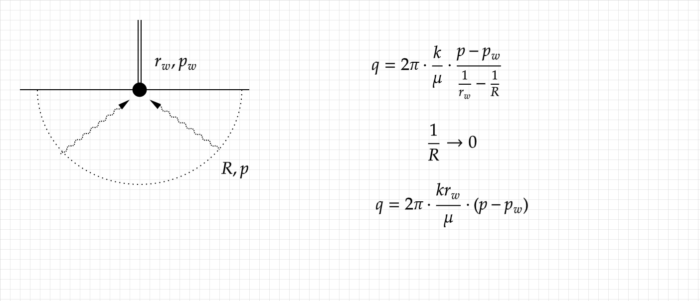
10. Для установившегося режима фильтрации нет разницы в какую из сторон рассматривать течение, поэтому проще всего вывести формулы для нагнетательной скважины. Надо мысленно представить, как через скважину закачивается в пласт вязкая нефть, и полученную форму закачанной пачки нефти приблизительно описать одним из типов фильтрации.

При смене типа фильтрации следует помнить, что давление в месте изменения остается постоянным. Это позволит склеить общее решение из множества типов фильтрации, через которые путешествует рассматриваемая пачка жидкости покидая скважину и пока не достигнет контура питания.