Slug Flow

Представленная статья «A Model for Gas-Liquid Slug Flow in Horizontal and Near Horizontal Tubes» (1975) Abraham E. Dukler и Martin G. Hubbard одна из самых часто цитируемых в области изучения природы двухфазного течения газа и жидкости. Испытывая наслаждение при ознакомлении с оригинальной статьей я решил представить свой вольный перевод, дополнив иллюстрациями из современных источников. Надеюсь и тебе она придется по душе, о мой читатель.

***

Пробковое течение (Slug Flow) представляет собой весьма сложный вид течения. Изучая фотоснимки, на которых последовательно запечатлены фазы движения жидкости и газа и применяя трассеры для подкрашивания потока, нами был раскрыт механизм этого явления. Предложенный подход подтвержден также и экспериментальными замерами давления вдоль горизонтальной трубы диаметром ~38 mm и длиной 19.8 m.

Визуальное наблюдение за процессом образования жидкостной пробки (снаряда) в трубе можно описать так.

1. Около точки ввода жидкости и газа наблюдается слоистое течение. При скорости подаваемого газа и жидкости близкой к моменту перехода к пробковому течению, за счет трения по длине трубы скорость жидкости замедляется. Уровень жидкости растет, стремясь достичь верхней точки сечения трубы. Одновременно с этим, на поверхности жидкости возникают волны. В какой то момент рост уровня жидкости совместно с ростом высоты волн становится достаточным, чтобы перекрыть на мгновенье сечение трубы, блокируя тем самым движение газовой фазы.

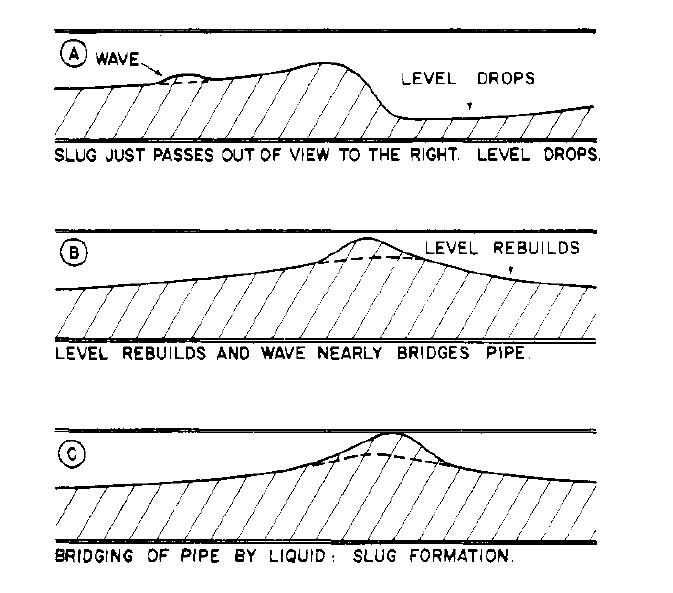
Слоистое течение с образованием волн на поверхности жидкости,

2. По всей видимости частицы жидкости образующие перемычку разгоняются по всему своему сечению до одинаковой скорости, образуя что-то похожее на ковш, который сгребает медленно движущуюся жидкость в тонком слое перед собой. Так быстродвижущаяся жидкость наращивает свой объем и превращается в сформированную пробку.

Полностью сформированная пробка показана на следующей схеме.

3. Сформированная пробка перемещается дальше по трубе, жидкость равномерно сбрасывается позади пробки и образует тонкий слой (плёнку, «film») со свободной поверхностью. Жидкость в пленке быстро замедляется за счёт трения со стенкой трубы и межфазному трению с газовой фазой (представлена зоной $l_f$ на схеме).

4. После формирования пробки, каждая следующая пробка поднимает жидкость тонкого слоя сброшенную прошлой пробкой. Скорость сброса и сгребания жидкости выравниваются, что приводит к стабилизации длины пробки.

5. При контакте с пробкой пленка проникает на некоторое расстояние в тело пробки, прежде чем окончательно ассимилируется в ней. Это явление обгона создает перемешивающий вихрь в передней части пробки. Интенсивное перемешивание приводит также к захвату некоторого количества газа (зона $l_m$ на схеме)

6. При увеличении скорости подачи газа, повышается степень аэрации в зоне перемешивания. В конечном счете, газ образует сплошную газовую фазу и начинает обтекать пробку. В такой момент пробка больше не в состоянии поддерживать перекрытие сечения и характер течения изменяется. Происходит переход к кольцевому режиму течения.

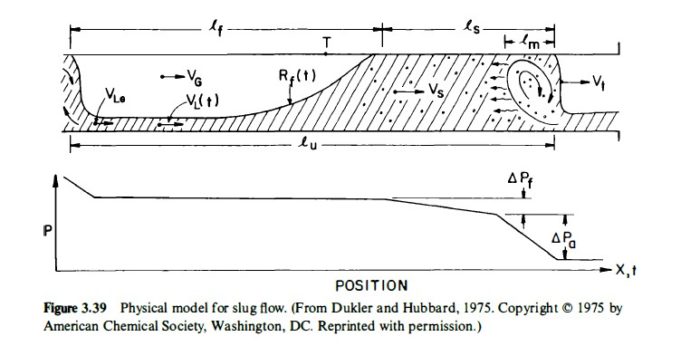
Идеализированный профиль давления подходящей представленной схеме пробкового течения должен выглядеть так.

В зоне смешивания наблюдается резкий рост давления, связанный с затратами энергии на ускорение пленочной жидкости. Далее следует линейное изменение давления в теле пробки, эквивалентное потерям давления которые наблюдались бы при течении жидкости, в которой распределены газовые пузырьки. В пленочной зоне давление остается практически не изменными, так как потери давления намного ниже возникающих потерь в пробке.

Рассмотрим типичные показания датчика снятые в точке Т.

При низкой скорости течения, скорость пленки и пробки сопоставимы друг с другом, потери давления на ускорение меньше чем потери давления в пленочной зоне. Здесь $\Delta p_m$ это потери давления в зоне смешивания, которые также называются потерями на ускорение $\Delta p_a$ .

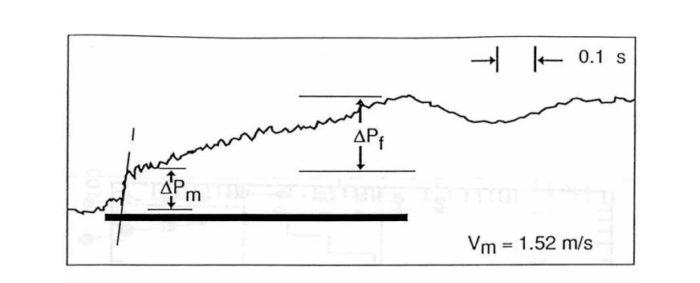
Следующая запись сделана для равных потерь в пленке и пробке,

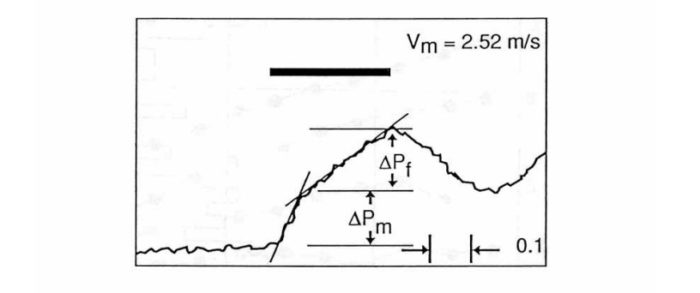
Случай очень высокой скорости в пробке и низкой скорости пленки, основные затраты энергии расходуются на разгон.

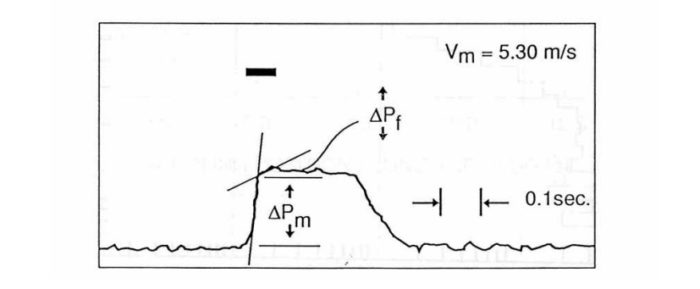
Время в течении которого жидкостная пробка проходит в месте установки датчика отмечено жирной, черной линией.

Очевидно, что пробковое течение имеет характер случайного процесса. В частности, время и расстояние между прохождением пробки действительно различаются, перепад давлениях в пробке, скорость движения пленки и другие функции подвержены случайным отклонениям. Нами не было найдено удовлетворительного описания формы распределения отклонения, однако экспериментальные данные показали, что полученные распределение вероятности достаточно узкие, что позволяет считать каждую расчетную характеристику потока как среднее значение для множества значений.

Общие потери давления в жидкостной пробке складываются из потерь на ускорение $\Delta p_a$ и потерь на трение об стенку трубы $\Delta p_f$ . Потерями давления в газовой фазе над пленкой жидкости пренебрежем.

$\Delta p_s = \Delta p_a + \Delta p_f$

Потери на ускорение
Стабильная пробка представляет собой тело постоянной длины, получающее и теряющее массу жидкости с равной скоростью. Скорость жидкости в пленке перед её подъемом ниже чем скорость движения пробки, поэтому требуется затратить усилия для её разгона. Сила, которая требуется для ускорения массы жидкости,

$\Delta F=ma = m \cdot \frac{V_s - V_{fe}}{\Delta t}$

Здесь $V_s$ это средняя скорость течения жидкости в пробке, $V_{fe}$ это средняя скорость течения жидкости в пленке перед пробкой. Сила прилагается в зоне смешивания, которая проникает на расстояние $l_m$ в тело пробки.

Изменение давление связанное с изменением скорости, относится к заполненному полностью сечению трубы $A$

$\Delta F = \Delta p_a \cdot A = m \cdot \frac{V_s - V_{fe}}{\Delta t}$

Обозначим через $x = m / \Delta t$ массовый расход с которым жидкость поступает в пробку.

$\Delta p_a = \frac{x}{A} \cdot (V_s - V_{fe})$

Потери на трение
Предполагая, что после прохождения вихревой зоны смешивания, обе фазы жидкость и захваченные пузыри газа однородно перемешиваются и движутся с одной скоростью, как одна фаза, потери на трение составят,

$\Delta p_f = \frac{2 \cdot f_s \cdot \rho_s \cdot V_s^2 (l_s - l_m)}{D}$

Средняя плотность жидкости в пробке

$\rho_s= \rho_L R_s + \rho_G (1-R_s)$

где под $R_s$ понимается объемное содержание жидкости в пробке (holdup).
Для определения коэффициента трения используется например корреляция Hall для шероховатых труб

$f_s = 0.001375\left(1+\left(2 \cdot 10^4 \frac{\epsilon}{D} + \frac{10^6}{Re}\right)^{1/3}\right)$

Число Рейнольдса определяется также из средней плотности и средней вязкости,

$\mu_s= \mu_L R_s + \mu_G (1-R_s)$

$Re_s = \frac{\rho_s D V_s}{\mu_s}$

Таким образом, для вычисления суммы потерь давления требуется определить следующие понятия

$x$ — массовая скорость подъема и сброса жидкости
$V_{fe}$ — скорость течения пленки, перед входом в пробку
$V_s$ — средняя скорость течения пробки
$R_s$ — объемное содержание жидкости в пробке
$l_s$ — длину пробки
$l_m$ — длину зоны смешивания и разгона.

Скорость течения пробки $V_s$
Рассмотрим движение пробки жидкости по трубе с постоянной скоростью $V_s$

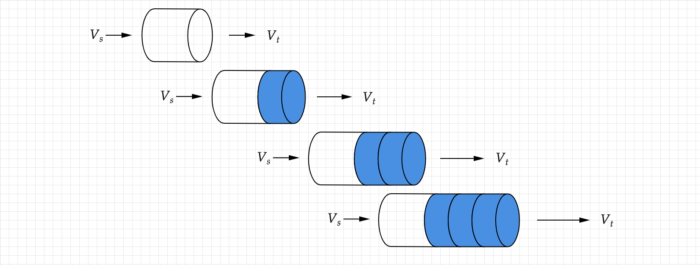
Каждый момент времени спереди пробки добавляется часть поднятой жидкости, которая тоже движется с постоянной скоростью $V_s$ . Если оценить скорость движения пробки по фронтальной поверхности, она окажется выше и более того, постоянно возрастает за счет добавляемого объема поднимаемой жидкости.

Общая длина пробки за счет этого постоянно растёт.

Другой пример это железнодорожный состав, где все вагоны движутся с постоянной скоростью $V_s$ и в равные промежутки времени перед составом добавляются несколько вагонов.

Теперь представим, что с другого конца пробки сбрасывается ровно такое же количество жидкости что и добавляется спереди. Или отцепляются вагоны с хвоста состава.

Получается, что отдельный вагон или частица жидкости внутри пробки движется с постоянной скоростью $V_s$ совершая трение об стенку трубы, а сама пробка или состав целиком движется гораздо быстрее со скоростью $V_t$ .

Поэтому скорость перемещения $V_t$ складывается из скорости движения в пробке $V_s$ и дополнительной скорости, возникающей из за появления объема спереди пробки в единицу времени. Дополнительная скорость определяется из массового расхода с которым жидкость из пленки поступает в тело пробки.

$V_t = V_s + \frac{x}{\rho_L A R_s}$

Отношение скорости поступления жидкости из пленки к скорости движения пробки обозначим как,

$C = \frac{x}{\rho_L A R_s} \cdot \frac{1}{V_s}$

Что упростит запись для скорости перемещения,

$V_t = (1 + C) V_s$

Полагая, что газ и жидкость не сжимаемы объемный расход смеси жидкости и газа через любое сечение трубы сохраняется постоянным,

$q_L+q_G = const$

Что позволяет выразить скорость течения в пробке, равной скорости подачи жидкости и газа на вход в трубу $V_m$

$V_m = \frac{q_L+q_G}{A} = V_s$

Величину $V_s$ можно определить из заданных расходов и диаметра трубы и более того, скорость не зависит от пропорции в которой единица пробкового течения $l_u$ делится на пленочную область $l_f$ и пробочную область $l_s$ .

Массовая скорость подъема и сброса жидкости x
Количество массы жидкости из пленки, которое будет поднято в зону смешивания зависит от разницы скорости с которой пробка догоняет пленку жидкости,

$x =\rho_L A R_{fe} ( V_t-V_{fe})$

Профиль локальных скоростей в теле пробки распределен от нулевой скорости на стенке трубы, до некоторой максимальной скорости в центральной линии течения.
Существует такое расстояние от центральной линии $r_p$ на котором скорость течения равна $V_s$ . Для региона $(r < r_p)$ локальные скорости превышают $V_s$ и частицы жидкости сохраняют направление течения. Для региона $(r > r_p)$ жидкость движется медленней, частицы жидкости в этом регионе отстают и сбрасываются из тела пробки.

Величина $C$ связана с этим геометрическим объемом,

$C =1 - \frac{2}{R^2} \int_0^{r_p} \frac{V(r)}{V_s}r dr$

Используя гипотезу о локальном кинематическом подобии поля турбулентных пульсаций скорости фон Кармана («Law of the Wall»), получим приблизительную апроксимацию зависимости коэффициента $C$ от величины числа Рейнольдса.

$C = 0.021 \cdot ln(Re_S) + 0.022$

Гидродинамика пленочной области
Форма поверхности жидкости в пленочной области представляет собой сложную трехмерную фигуру, точное описание которой по всей видимости не может быть найдено. Авторы предлагают следующее приблизительное описание.

Рассмотрим элемент пленки размером $\Delta x$ заключенный между сечением 1 и 2.

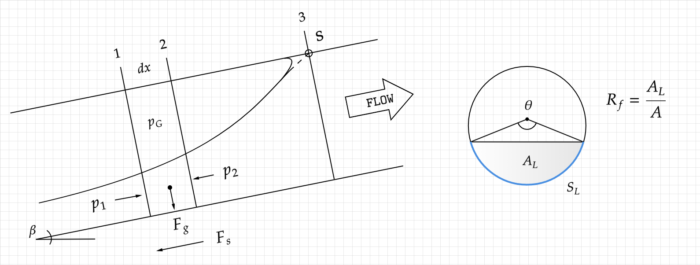
Площадь сечения, занятого жидкостью

$A_L = R_f \cdot A$

Масса жидкости в элементе,

$m = \rho_L \cdot A_L \cdot \Delta x$

Слева и справа на элемент действует сила давления приложенная к сечению жидкости. Давление зависит от суммы давления в газе над жидкостью и гидростатического давления,

$p_1=p_G+\rho_L g (\xi D)$

Точка приложения силы смещена ниже центра тяжести на величину эксцентриситета . В статье «Gravity currents and related phenomena» (Brooke Benjamin, 1968) приведено решение,

$\xi=-\frac{1}{2}cos\left(\frac{\theta}{2}\right)+\frac{1}{3\pi R_f} sin^3\left(\frac{\theta}{2}\right)$

где угол связан с объемной долей жидкости соотношением,

$R_f = \frac{\theta-sin\theta}{2\pi}$

Если труба имеет наклон к горизонту на элемент также действует проекция силы тяжести,

$F_g = mg (sin \beta) = \rho_L \cdot A_L \cdot \Delta x \cdot g \cdot (sin \beta)$

Сила трения жидкости об стенку трубы, направлена противоположно течению,

$F_s = \tau_w \cdot S_L \cdot \Delta x$

где $S_L$ это смоченный периметр трубы.

Рассмотрим относительную систему координат сечения 3, полагая точку $S$ не подвижной. Тогда точка $S$ движется с той же самой скоростью, что и фронтальная поверхность пробки $V_t$ . Мимо неё проплывает пленка с относительной скоростью,

$\omega_f = V_f - V_t$

и тело пробки течет медленней точки $S$ с относительной скоростью,

$\omega_s = V_s - V_t$

Материальный баланс связывающий сечение 3 с произвольным сечением в пленочной области,

$\omega_s R_s \rho_L A = \omega_f R_f \rho_L A$

Получим зависимость между $R_f$ и $V_f$ ,

$V_f(x) = V_s \left(1 - C \cdot \frac{R_s - R_f(x)}{R_f(x)}\right) = B\cdot V_s$

Изменение импульса (относительной скорости потока) между сечением 1 и 2 связано с изменением суммы действующих сил.

$ma = \sum F$

$\frac{(m\omega_f)_2-(m\omega_f)_1}{\Delta t} = \sum F$

Вспоминая, что массовый расход жидкости записывается как,

$W_L = \rho_L \cdot V_f \cdot A_L = \frac{m}{\Delta t}$

Получим,

$(\rho_L \cdot V_f \cdot A_L (V_f-V_t))_2 - (\rho_L \cdot V_f \cdot A_L(V_f-V_t))_1 =$

$\left[\rho_L g (\xi D)_1 - \rho_L g (\xi D)_2\right] \cdot A_L -\tau_w \cdot S_L \cdot \Delta x - \rho_L \cdot A_L \cdot \Delta x \cdot g \cdot sin \beta$

Перейдем к пределу, сближая сечения 1 и 2 друг к другу

$\frac{d(V_f(V_f-V_t) \cdot R_f)}{d x} = gD \cdot \frac{d( \xi \cdot R_f)}{dx} -\tau_w \cdot \frac{S_L }{A \cdot \rho_L} - R_f \cdot g \cdot sin \beta$

Здесь под $V_f$ понимается средняя скорость течения пленки через сечение $A\cdotR_f$ .

Касательное напряжение трения жидкости об стенку трубы, зависит от коэффициента трения

$\tau_w = f_f \frac{\rho_L V_f^2}{2}$

Коэффициент трения, зависит от числа Рейнольдса

$Re_f = \frac{2 \pi B R_f}{\theta} \cdot Re_s$

Смоченный периметр,

$S_L = \frac{\theta D}{2}$

Решение дифференциального уравнения сводится к численному интегрированию уравнения из которого следует определить $R_{fe}$ ,

$\int_{R_f}^{R_s} W(R_f)dR_f = \frac{l_f-x_f}{D}$

где $W$ зависит от $R_f$ и изменяется вдоль пленки.

В точке $x_f=0$ перед подъемом жидкости в пробку $R_f = R_{fe}$ . В точке $S$ значение $x_f = l_f$ и $R_f = R_s$ .

Запись для функции $W$ следующая,

(1) $\begin{multline*} W = \left(\frac{C^2R_s^2}{R_f^2} - \frac{1}{Fr}\left(\frac{\pi}{2}R_f \, \sin \frac{\theta}{2} + \sin^2 \frac{\theta}{2} \cos\frac{\theta}{2} \right) \cdot \frac{1}{1-\cos \theta} - \frac{1}{2} \, \cos \frac{\theta}{2}\right) \\ \cdot \frac{1}{\displaystyle f_f B^2 \frac{\theta}{\pi}+\frac{R_f}{Fr} \sin \beta} \end{multline*}$

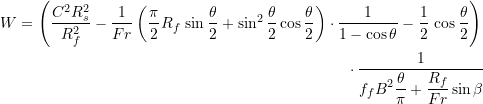
здесь

$B = 1 - C \cdot \frac{R_s - R_f(x)}{R_f(x)}$

$Fr = \frac{V_s^2}{g D}$

Перед интегрированием требуется задать величину $l_f$ .
Процедура начинается с вычислением $W$ при значении $R_f=R_s$ и продолжается добавлением $\Delta R_f$ до тех пор, пока значение интеграла не приравняется правой части.

Полученное значение $R_f$ и будет искомым $R_{fe}$ .

Длина пробкового и пленочного региона

Пусть время прохождения пробкового региона относительно некоторого сечения равно $T_s$ и время за которое проходит пленочная область $T_f$ . Сумма этих времен, определяет частоту прохождения пробки $\nu_s = 1 / (T_s + T_f)$ .

Общая длина единицы (unit) пробкового течения,

$l_u = \frac{V_t}{\nu_s}$

Длина пленочного региона,

$l_f = (l_u-l_s)=\frac{V_t}{\nu_s}-l_s$

Масса жидкости, переносимая пробкой,

$M_s = \int_0^{T_s} V_s A R_s \rho_L dt = V_s A R_s \rho_L T_s$

заменяя

$T_s = \frac{l_s}{V_t}$

получим,

$M_s = V_s A R_s \rho_L \frac{l_s}{V_t}$

Аналогично для пленочного региона,

$M_f = \int_0^{T_f} V_f A R_f \rho_L dt$

заменяя,

$t = \frac{x_f}{V_t}$

получим,

$M_f = \int_0^{l_f} V_f A R_f \rho_L \frac{1}{V_t}dx_f$

Делая замену переменной скорости пленки $V_f$ , получим ещё одно тяжелое уравнение,

$\frac{W_L}{\rho_L A V_s} = \frac{\nu_s}{V_t}\left(R_s \cdot l_s +\int_0^{l_f} (R_s - R_f)dx_f\right)$

здесь $W_L$ это массовый дебит жидкости, кг/c.

Выражая $l_s$ из приведенного уравнения, возникает следующий интеграл,

$I=\int_0^1 \frac{R_f(1+C)-CR_s}{R_{fe}(1+C)-CR_s}d \left(\frac{x_f}{l_f}\right)$

Проведенные расчеты показали, что значение $I$ стремится к $1$ при всех условиях течения. Такое поведение подтверждается и наблюдением — толщина пленки резко падает до значения $R_{fe}$ позади пробки на небольшом расстоянии, уменьшаясь затем совсем незначительно.

Принимая $I = 1$ , длина пробкового региона

$l_s=\frac{V_s}{\nu_s(R_s-R_{fe})}\left(\frac{W_L}{\rho_LAV_s}-R_{fe}+C(R_s-R_{fe})\right)$

Длина зоны смешивания $l_m$
Размер зоны проникновения жидкости пленки в тело пробки, представляется зависящим от относительной скорости между движения пробки и пленки $(V_s-V_{fe})$ . Это наблюдение основывается на физической основе подтвержденной высокочастотной съемкой и фотографией. Простой способ оценки может быть получен через концепцию «скорости напора»,