Slug Flow практика

Попробуем освоить практику расчета slug flow.
В качестве исходных данных, я взял срез данных из GAP для элемента трубы.

Плотность жидкости, $\rho_L$ = 791.1 kg/m3
Плотность газа, $\rho_G$ = 20.127 kg/m3
Вязкость жидкости, $\mu_L$ = 5.5253 mPa*s
Вязкость газа, $\mu_G$ = 0.010344 mPa*s

Массовый расход жидкости, $W_L$ = 27.1658 kg/s
Массовый расход газа, $W_G$ = 2.94884 kg/s

Диаметр трубы, $D$ = 0.3048 m
Шероховатость трубы, $\epsilon$ = 1.52E-05 m.

Расчет требует следующих исходных данных,

Частота прохождения пробки, $\nu_S$ = 0.40476 1/min = 0.006746 1/s
Объемное содержание жидкости в пробке, $R_s$ = 0.83854

Что можно посчитать сразу.

Площадь сечения трубы, $A = \pi D^2 / 4$ = 0.072964 m2
Скорость течения пробки,

$V_s = \frac{1}{A} \left(\frac{W_L}{\rho_L} + \frac{W_G}{\rho_G}\right)=2.4786\,m/s$

Средняя плотность в пробке, $\rho_S=\rho_L R_s+\rho_G(1-R_s)$ = 666.62 kg/m3
Средняя вязкость в пробке, $\mu_S=\mu_L R_s+\mu_G(1-R_s)$ = 4.635 mPa*s

Число Рейнольдса, $Re_s = \rho_S D V_s / \mu_S$ = 108660
Коэффициент трения тела пробки со стенкой трубы, $f_s$ = 0.00605

Коэффициент $C = 0.021 \cdot ln(R_s) + 0.022$ = 0.2655

Определим скорость перемещения пробки, $V_t = (1+C)V_s$ = 3.136 m/s
И общую длину единицы течения пробки, $l_u = V_t / \nu_S$ = 464.98 m

Построение распределения объемного содержания жидкости с расстоянием от конца пробки, связано с интегрированием функции $W$

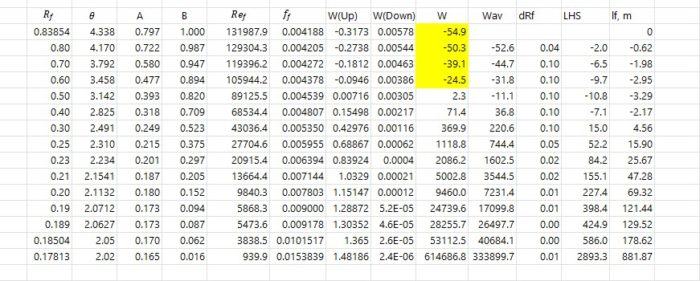
Обращает внимание, что в самом начале пленочного региона значение функции $W$ принимает отрицательные значения. Такое поведение описано в 1978 M. K. Nicholson, K. Aziz and G. A. Gregory «Intermittent Two Phase Flow in Horizontal Pipes: Predictive Models».

«В работе определено, что положительное значение функции $W$ наблюдается только для скорости $V_m$ большей критической скорости $V_m^*$ , которое пропорционально диаметру трубы для данных свойств флюидов. При значениях $V_m < V_m^*$ необходимо уменьшать значение $R_f$ до тех пор, пока функция $W$ не станет положительной. Пленочный регион начинается с полученного значения $R_f$ и соответствующей скорости $V_f$ , которые не равны предложенным Duckler и Hubbard начальным условиям.»

В ходе нескольких итераций, определено значение $R_{fe}$ = 0.189,
соответствующая ему длина пробочного региона $l_s$ = 98.05 m
и длина пленочного региона $l_f=l_u-l_s$ = 366.9 m.