Smooth Stratified Flow
Статья «A Model for Predicting Flow Regime Transitions in Horizontal and Near Horizontal Gas-Liquid Flow» (1976) авторов Abraham E. Dukler и Yemada Taitel состоит из нескольких частей. В первую очередь в ней дается описание гладкого слоистого течения.
***
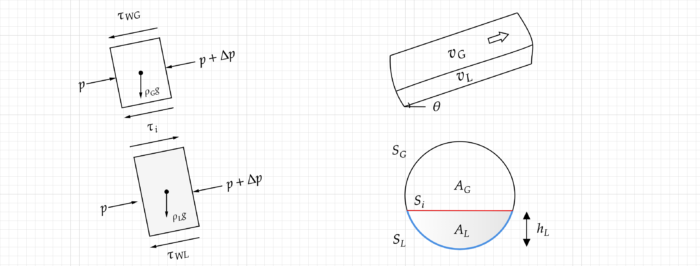
Рассмотрим силы действующие на газовую и жидкую фазу при невозмущенном, слоистом течении.
Элемент трубы имеет наклон ![]() к горизонту, газ и жидкость перемещаются со средней скоростью
к горизонту, газ и жидкость перемещаются со средней скоростью ![]() и
и ![]() . В сечении трубы выделим следующие геометрические параметры. Площадь занятая газом и жидкостью обозначим как
. В сечении трубы выделим следующие геометрические параметры. Площадь занятая газом и жидкостью обозначим как ![]() и
и ![]() . Смоченный периметр трубы
. Смоченный периметр трубы ![]() и
и ![]() . Длина поверхности раздела между фазами обозначим как
. Длина поверхности раздела между фазами обозначим как ![]() .
.
Уровень жидкости в условиях равновесия ![]() .
.
Исходя из известных скоростей течения фаз, свойств, угла наклона и диаметра трубы, требуется определить значение ![]() .
.
Для жидкости, изменение скорости при перемещении элемента на расстояние ![]() связано с потерями давления на трение жидкости со стенкой трубы (wall-liquid, wl), ускорением за счет трения с быстроперемещающейся газовой фазой и затратами на преодоление силы тяжести.
связано с потерями давления на трение жидкости со стенкой трубы (wall-liquid, wl), ускорением за счет трения с быстроперемещающейся газовой фазой и затратами на преодоление силы тяжести.
![]()
Для газа,
![]()
Приравнивания падения давления в фазах друг другу и предполагая, что изменением давления по ![]() можно пренебречь, получим
можно пренебречь, получим
![]()
Записанное равенство напряжений позволяет подобрать значение ![]() , которое неявно входит в это выражение через площади и смоченные периметры. Это реализуется итерационной процедурой.
, которое неявно входит в это выражение через площади и смоченные периметры. Это реализуется итерационной процедурой.
Касательное напряжение трения между жидкостью и трубой (Wall-Liquid),
![]()
Коэффициент трения для гладкой трубы, зависит от числа Рейнольдса
![]()
Для газа запись аналогична (Wall-Gas),
![]()
Коэффициент трения для гладкой трубы, зависит от числа Рейнольдса
![]()
Для ламинарного режима течения ![]() и
и ![]() .
.
Для турбулентного режима ![]() и
и ![]() .
.
Гидравлические диаметры определяются из подхода предложенного Agrawal (1973). Сопротивление течения жидкости аналогично потоку в открытом канале, для газа аналогично потоку в закрытом канале.
![]()
![]()
Касательное напряжение между газом и поверхностью раздела,
![]()
Согласно работе Gazley (1949), для слоистого течения, коэффициент трения между фазами примерно равен коэффициенту трения газа о стенку трубы
![]()
И принимая во внимание, что скорость течения газа намного больше скорости перемещения границы раздела фаз, получим выражение совпадающее с записью касательного напряжения на границе газ-труба,
![]()
Представленные выше соотношения позволяют решить задачу определения потерь давления и доли жидкости в сечении трубы для гладкого расслоённого режима течения.
Между геометрическими параметрами и уровнем жидкости существует непростая связь,
![]()
![]()
![]()
![]()
![]()
Следующий пример поможет понять логику расчета слоистого течения. В качестве исходных данных, я снова взял срез данных из GAP для элемента трубы.
Плотность жидкости ![]() = 800.6 kg/m3
= 800.6 kg/m3
Плотность газа, ![]() = 13.53 kg/m3
= 13.53 kg/m3
Вязкость жидкости, ![]() = 6.4771 mPa*s
= 6.4771 mPa*s
Вязкость газа, ![]() = 0.0102 mPa*s
= 0.0102 mPa*s
Массовый расход жидкости, ![]() = 27.056 kg/s
= 27.056 kg/s
Массовый расход газа, ![]() = 1.608 kg/s
= 1.608 kg/s
Диаметр трубы, ![]() = 0.3048 m
= 0.3048 m
Шероховатость трубы, ![]() = 1.52e-5 m
= 1.52e-5 m
Рассчитаем площадь трубы, ![]() = 0.07296 m2
= 0.07296 m2
Задаем величину уровня жидкости в трубе.
Начнем с предположения, что половина трубы занята жидкостью ![]() = 0.5
= 0.5
Периметр смоченный газом, ![]() = 0.4788 m
= 0.4788 m
Периметр смоченный жидкостью, ![]() = 0.4788 m
= 0.4788 m
Длина поверхности раздела, ![]() = 0.3048 m
= 0.3048 m
Теперь определим площади занятые жидкой и газовой фазами,
![]()
![]()
Доля жидкости в сечении трубы,
![]()
Зная величину ![]() можно рассчитать истинные скорости течения,
можно рассчитать истинные скорости течения,
![]()
![]()
Знание скоростей, позволит нам определить коэффициенты трения.
Для этого сначала вычислим гидравлические диаметры,
![]() = 0.3048 m
= 0.3048 m
![]() = 0.1862 m
= 0.1862 m
Числа Рейнолдьса,
![]() = 34 900
= 34 900
![]() = 805 724
= 805 724
И жидкость и газ движутся турбулентно, коэффициенты трения об стенку трубы следовательно
![]() = 0.00568
= 0.00568
![]() = 0.00303
= 0.00303
Касательное напряжение трения жидкость-труба,
![]() = 1.9504
= 1.9504
Касательное напряжение трения газ-труба,
![]() = 0.2175
= 0.2175
Касательное напряжение межфазного трения,
![]() = 0.2175
= 0.2175
Для горизонтальной трубы, баланс между силами трения запишется в виде,
![]()
Левая часть уравнения, после подстановки значений переменных, равна ![]() 3.634 и соответственно правая часть,
3.634 и соответственно правая часть, ![]() = 22.7403. Повторяя итерации
= 22.7403. Повторяя итерации ![]() проводится поиск равенства левой и правой части уравнения.
проводится поиск равенства левой и правой части уравнения.
После нескольких попыток, определено искомое значение ![]() = 0.61436 при котором значение доли жидкости равно
= 0.61436 при котором значение доли жидкости равно ![]() .
.
Удельные потери давления можно определить как по жидкой так и по газовой фазе. Используем уравнение сохранения для жидкой фазы.
![]()
Подставляя значения, потери на трение составили 11.442 Pa на 1 метр трубы.
В GAP получено большее значение 17.54 Pa
Меньшие потери вызываны тем, что расчет потерь давления выполнен для гладкого слоистого течения, при котором поверхность жидкости представлена ровной поверхностью. Тогда как в зависимости от соотношения скоростей газа и жидкости на поверхности раздела возникают волны. От высоты формируемой волны, поверхность жидкости становится более сложной и выражение для коэффициента трения между жидкой и газовой фазой усложняются.