Надо написать видимо какое-то вступление.

Современный инженер-разработчик связанный с моделированием, часто имеет дело с поиском зависимостей. Огромную пользу в этом деле приносит инструментарий excel «добавить линию тренда», где выбор между типом тренда зависит от коэффициента детерминации R². Для значений эр-квадрат от 0.5 и выше апроксимирующая функция считается годной к использованию.

Вы обязательно встретите коэффициент детерминации при масштабировании фазовых проницаемостей, где я и сделал следующее наблюдение. Мной были сделаны усилия вывести точное рассуждание, но увы отступив и опасаясь потерять найденные примеры, излагаю далее как есть.

Первый пример связан с остаточной нефтенасыщенностью.

Можно ожидать, что чем хуже коллекторские свойства тем остаточная нефтенасыщенность выше. Однако фактические данные показывают, что остаточная нефтенасыщенность при вытеснении водой почти не зависит от коллекторских свойств или зависит очень слабо. Коэффициент R² бывает очень низкий, порой даже тренд меняет направление и кажется, что остаточная нефтенасыщеность тем ниже, чем хуже коллекторские свойства.

Не обнаружив значимых трендовых зависимостей, в моем случае решено остановится на начальной водонасыщенности Sw как определяющем факторе,

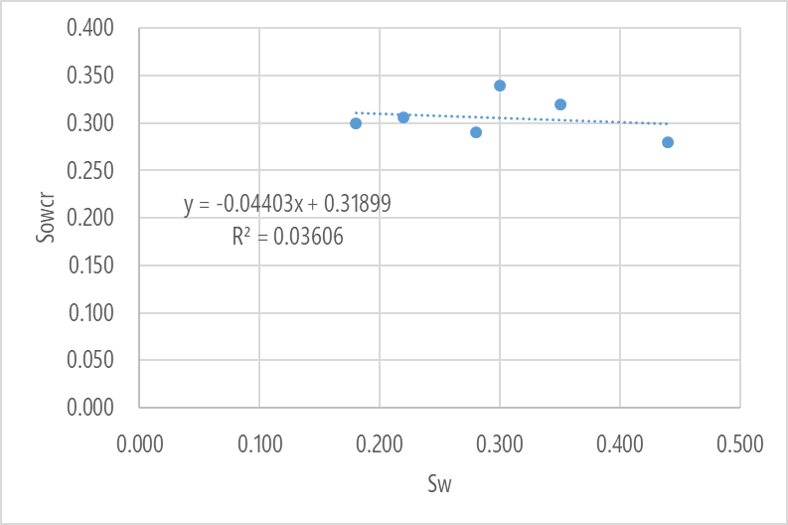
Значение R²=0.03606 говорит о том, что Sowcr слабо зависит от Sw. И это видно глазами.

Однако далее, был найден комплекс величин «коэффициент вытеснения», в который входит Sowcr и который обладает значительным R²=0.7890. Поэтому, предложен следующий порядок вычислений — по заданному Sw определяется Квыт из которого выражается Sowcr и присваивается ячейкам модели.

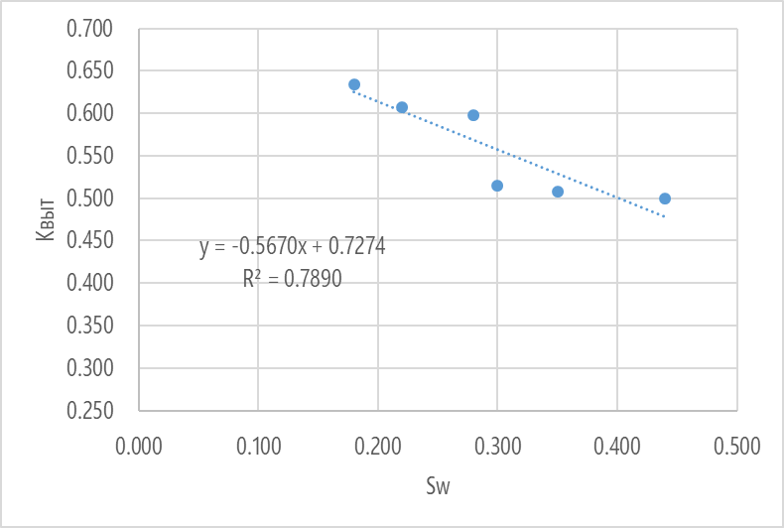
Здесь я сразу объясню суть моего наблюдения.

Коэффициент детерминации гарантировано улучшается, если искомую функцию замешать вместе с функциональной зависимостью от аргумента. Другими словами, начальный неудачный поиск

   

подменяется на

   

очевидно, что

   

имеет коэффициент детерминации равный 1, поэтому итоговый коэффицент R² улучшится, так как алгоритм регрессии чувствует занесенную извне функциональную зависимость.

С точки зрения самого апроксимирующего уравнения никакой особой разницы нет использовать ли исходную зависимость, либо «улучшенную» версию. Проблема в том, что инженер подменяет отсутствие зависимости уверенностью, что такая зависимость действительно существует. И делает это опираясь на значение коэффициента R², который именно для таких случаев является не достоверной оценкой.

Давайте проследим, как изменится R² если мы повторим предложенный порядок вычисления Sowcr.

Коэффициент вытеснения, это у нас

   

выше была найдена «уверенная» зависимость, которая запишется так,

   

устраним зависимость левой части от Sw и выразим чистый Sowcr

   

Как видно, под операцией с «коэффициентом вытеснения» скрыта квадратичная зависимость от начальной водонасыщенности.

К сожалению, при выборе полинома второй степени эксель предлагает другие коэффиценты, тем не менее можно подобрать уравнение близкой к искомому,

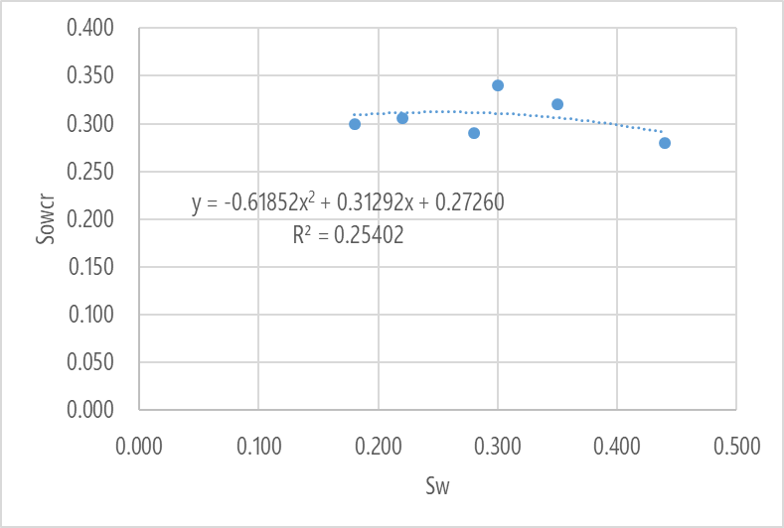
В целом полином лучше описывает исходные значения, но R² также остается ниже уровня уверенности и конечно же от R²=0.789 ни осталось и следа.

Второй пример связан с фазовой проницаемостью воды.

Одна из точек фазовых проницаемостей это относительная фазовая проницаемость по воде в присутствии остаточной нефтенасыщенности, черезвычайно важный параметр определяющий соотношение подвижности нефти и воды в пластовых условиях.

После поиска зависимости, решено остановится на абсолютной проницаемости как определяющем факторе,

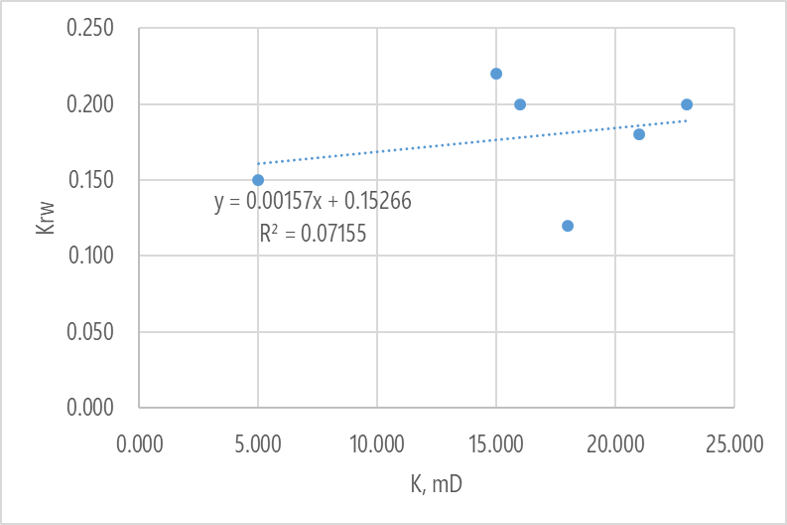
Однако коэффициент детерминации оставляет желать лучшего. Предложена следующая анаморфоза. Вместо относительной фазовой проницаемости по воде используется просто фазовая проницаемость по воде (в миллидарси),

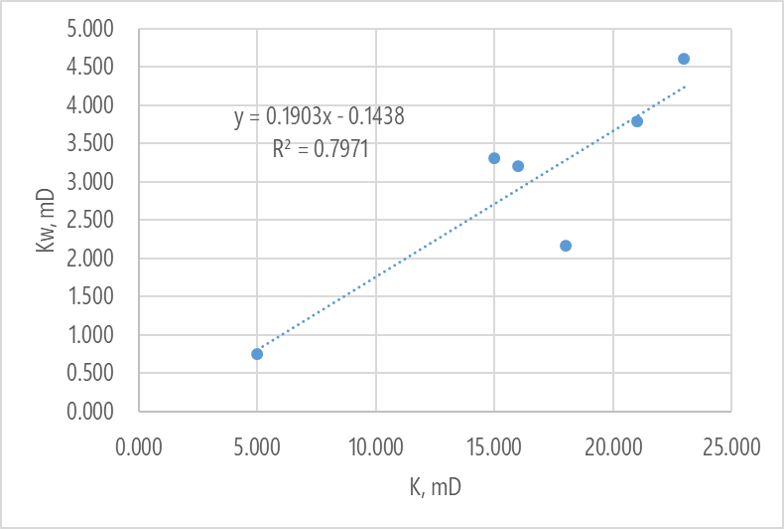
В итоге получена уверенная зависимость фазовой по воде от абсолютной проницаемости. И предложена следующая схема проведения расчета — по известному значению проницаемости K определяется сначала фазовая проницаемость по воде Kw, а затем уже и относительная фазовая проницаемость по воде, которая и закладывается в модель.

Давайте рассмотрим, что произошло.

Исходная зависимость, необладающая значимой связью имела вид

   

далее совершена подмена на следующую «принятую к действию» зависимость,

   

запишем, что же это за уравнение

   

выразим Krw

   

Таким образом, в подмененной модели рассматривается зависимость относительной фазовой проницаемости по воде от обратной абсолютной проницаемости. Проверим, насколько хорошо в таком случае апроксимируется исходные значения функцией,

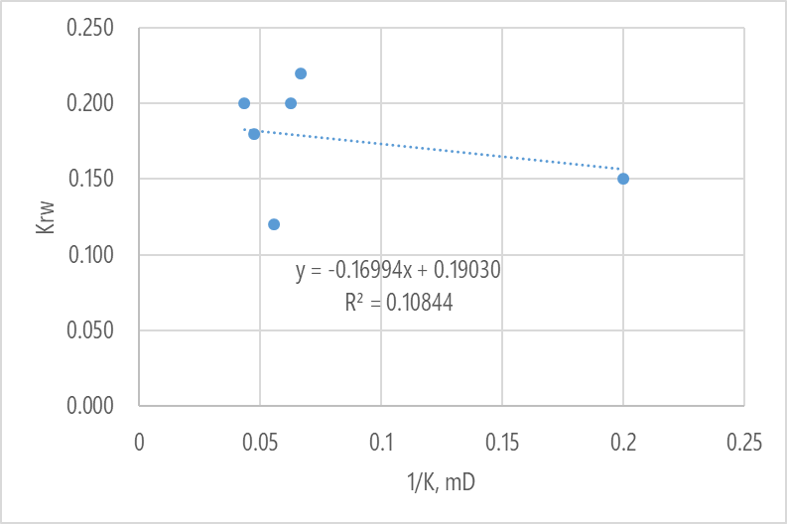
Как видно, коэффициент детерминации R² как был не значимым, так им и остался.

У этих двух историй есть один общий знаменатель, один общий пасс руками.

Искомая переменная, не имеющая значимой корреляции, подменяется некоторым комплексом имеющим высокий R² за счёт включения в комплекс аргумента функции. Далее, на основе высокого коэффициента детерминации делается вывод о состоятельности предложенного комплекса и совершается обратный переход от комплекса к искомой переменной. Таким образом, свойство комплекса распространяется на искомую переменную по ложному принципу наследственности.

Мне неизвестно как обезопасить себя от совершения подобного мыслепреступления, мной записаны эти два случая от инженеров, чья высокая квалификация не вызывает сомнений. А уж про нас то, о мой юный читатель, что и говорить…