Решение задач гидростатики
Рассмотрение задач статического равновесия жидкостей и газов начинается с выбора горизонтального уровня на котором давление остается постоянной величиной.
Вот несколько типичных примеров.

Запишем основное уравнение гидростатики для уровня 1-2
![]()
Первая часть уравнения, это давление действующее на жидкость со стороны внешних сил, в данном примере это только внешнее атмосферное давление и вторая часть, это давление создаваемое весом самой жидкости. Уровень жидкости в левом и правом сосуде одинаковый.
Далее усложним пример и добавим в левый сосуд нефть,
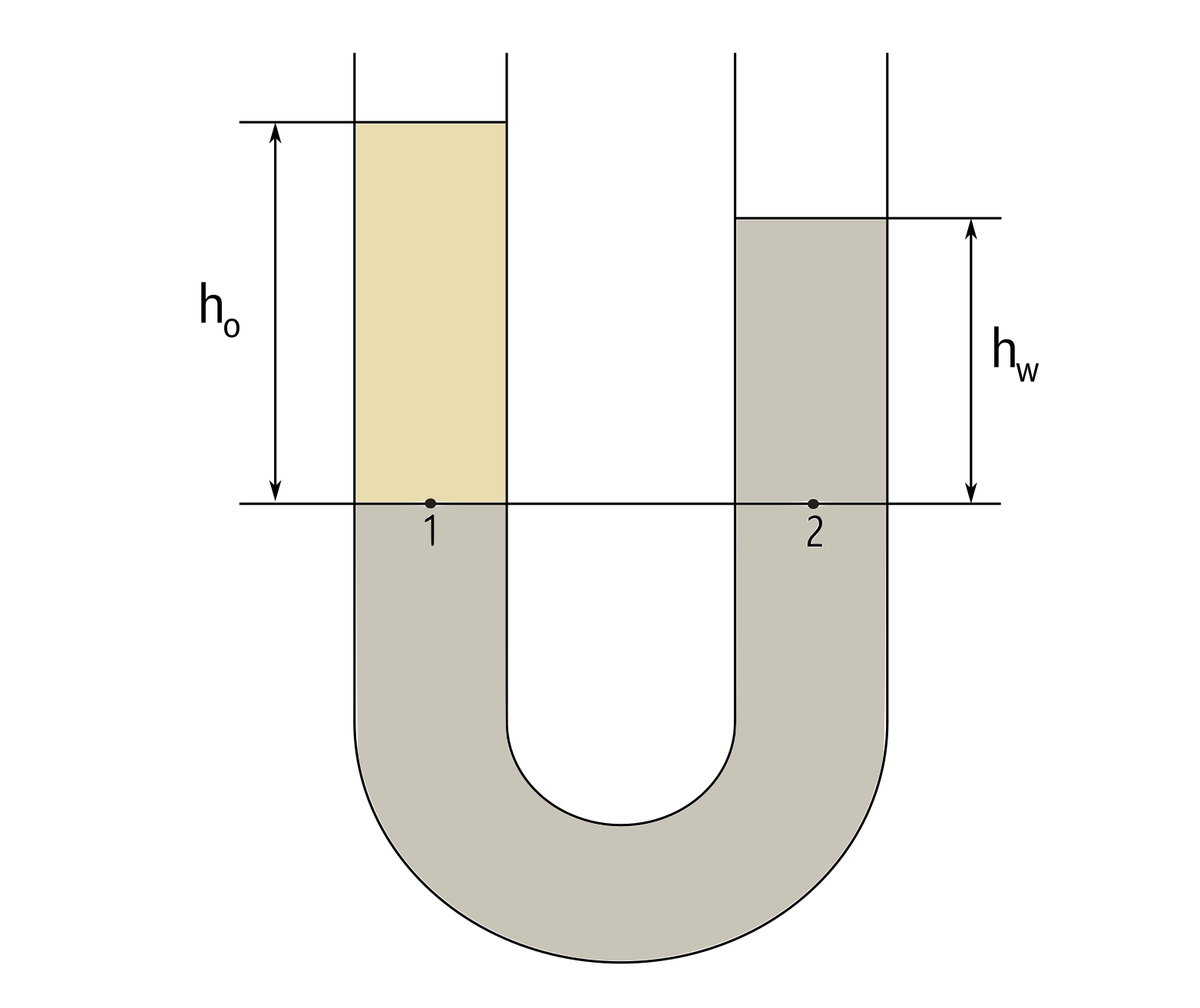
Уровень проведем по контакту нефть-вода. Запишем равновесие для первой и второй точки,
![]()
![]()
Приравняем давления,
![]()
Свойство жидкости или газа сохранять постоянную плотность (следовательно и давление) на одном потенциальном уровне от уровня земли, приводит к перераспределению уровня в сообщающихся сосудах. Одинаковое давление на уровне создается разным столбом нефти и воды.
![]()
Теперь давайте закупорим левый сосуд и закачаем газ под давлением,
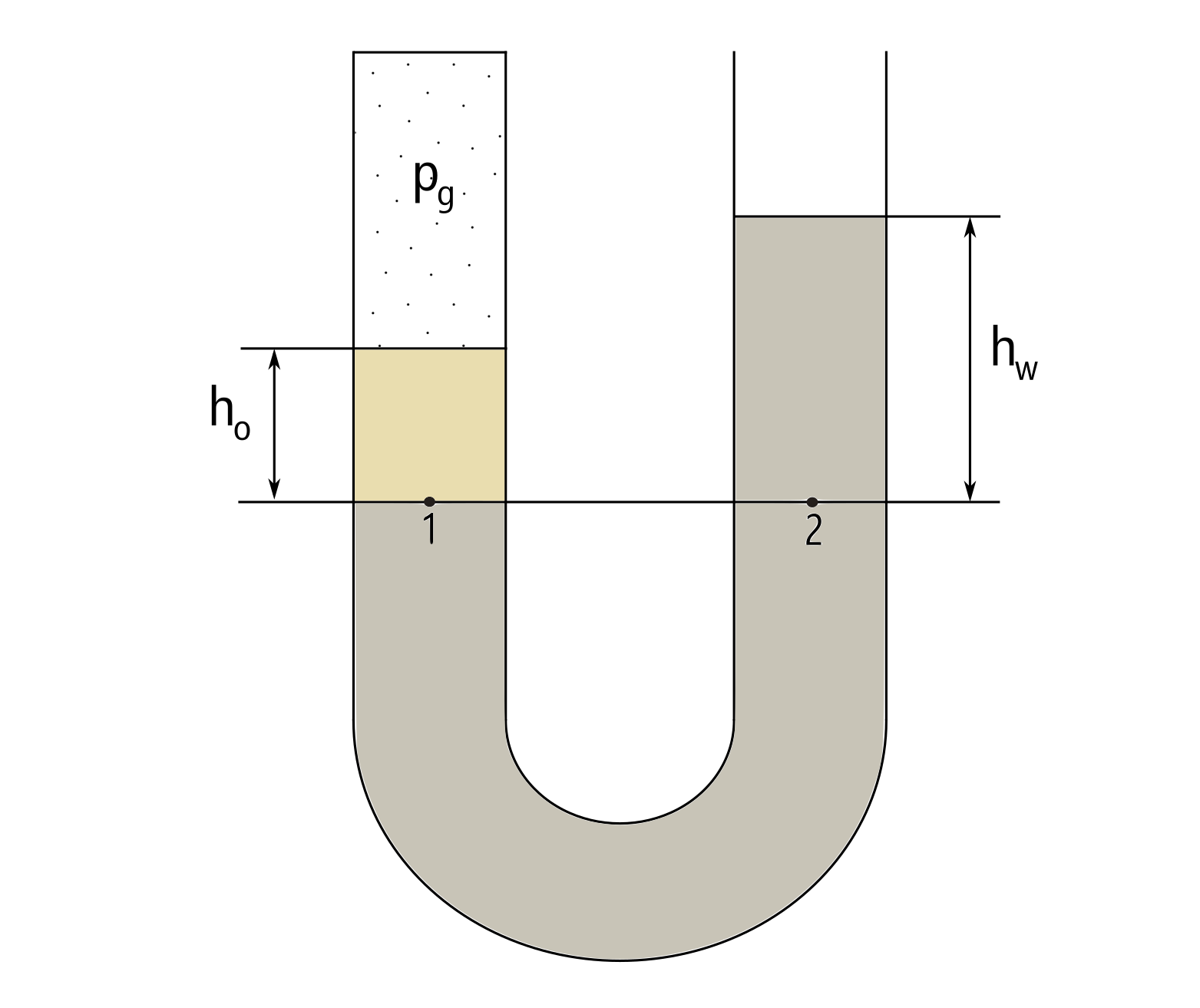
Давление в правом сосуде, также как и раньше определяется атмосферным давлением и высотой столба воды,
![]()
А в левом сосуде, атмосферное давление сменяется давлением газа над нефтью,
![]()
Вся эта история уравновешивает себя по уровню 1-2.
![]()
![]()
В инженерной практике не любят оперировать понятием атмосферное давление. Чаще используется величина «манометрическое давление», которое показывает превышение абсолютного давления над атмосферным.
![]()
Через манометрическое давление газа, уравнение равновесия запишется короче,
![]()
Разница в высоте уровней нефти и воды теперь зависит не только от разницы плотностей, но и от избыточного давления над нефтью.
Рассмотрим следующую геологическую ситуацию.
Две рядом лежащие нефтяные залежи, с газовыми шапками для общего рассуждения, относятся к одному водоносному горизонту. В данной схеме рассматривается положение уровня свободной воды (fwl) в левой и правой залежи,
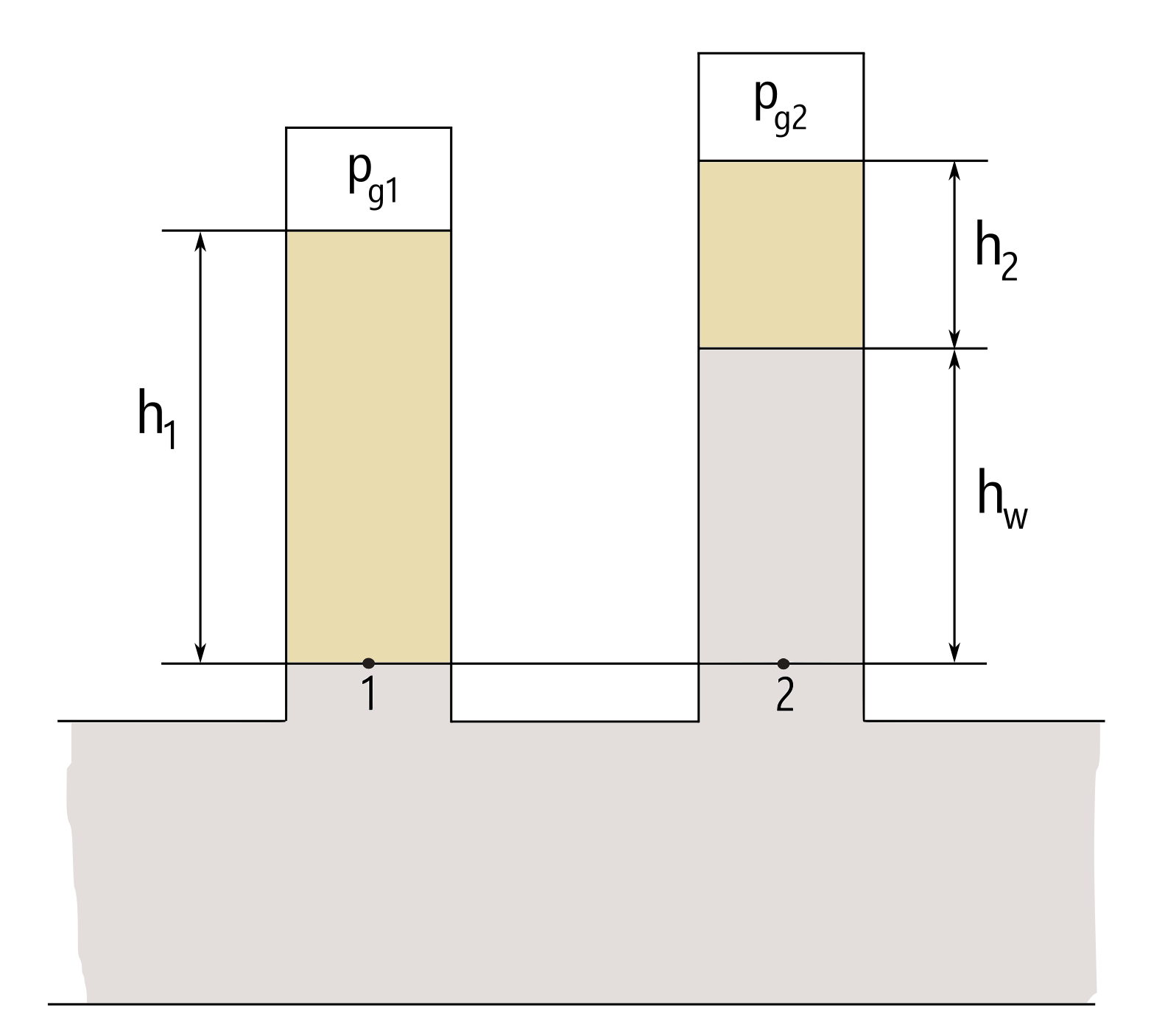
Давление в левой залежи на уровне 1-2 определяется весом столба нефти и избыточным давлением над жидкостью, создаваемое газовой шапкой,
![]()
Давление в правой залежи, состоит из давления газовой шапки над жидкостью плюс вес столба нефти и воды
![]()
Уравнение гидростатического равновесия,
![]()
![]()
Разница в уровнях свободной воды компенсируется весом столба воды и разницой давлений газовых шапок.
Следовательно, если две залежи неважно как далеко друг от друга расположенные, не имеют сообщения друг с другом по нефтяной части, уровень контакта (fwl) может быть разным. Более того, уровень контакта почти обязан быть разным, так как при формировании залежи нефть оттесняла воду вниз и положение контакта зависит от массы нефти в левой и правой части. Учитывая сложность формы залежей, вероятность наполнения залежей под один уровень маловероятное событие.
В случае отсутствия газовых шапок в любом случае необходимо сохранять величину избыточного давления над жидкостью в левой и правой залежах.
Хотелось бы, чтобы Вы оценили следующие тезисы:
1. Так называемый «наклонный контакт» (далее, «нк») объясняется Вашим данным анализом.
2. НК правильнее интерпретировать как ступенчатый?
3. НК возможен в залежах с множествами разломов, обязательно «режущие» и охватывающие всю нефтяную часть. И, «ступенчатость» контактов не возможна при равноудаленных разломах.
4. Клиноформенные залежи прямой геологический пример для Вашего анализа.