ОФП ещё раз про любовь

§1 Теория Баклея-Леверетта

Экспериментально установлено, что при фильтрации нефти и воды скорость фильтрации каждой фазы зависит от текущей водонасыщенности. Изменение скорости фильтрации учитывается дополнением уравнения Дарси понятием относительной фазовой проницаемостью,

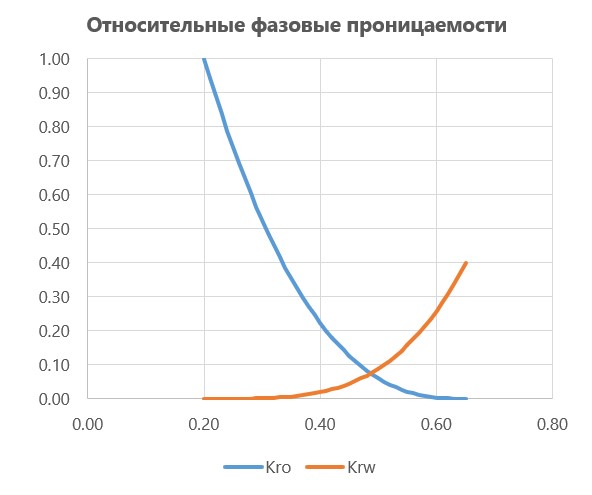
$v_o= k^*_o(S_w) \cdot \frac{k}{\mu_o} \cdot \frac{dp}{dx}$

$v_w= k^*_w(S_w) \cdot \frac{k}{\mu_w} \cdot \frac{dp}{dx}$

Типовые зависимости ОФП от насыщенности выглядят следующим образом,

При вытеснение нефти водой происходит рост водонасыщенности. Различие в скорости фильтрации приводит к тому, что закачиваемая вода, движется быстрее чем вытесняемая нефть. Образуется фронт вытеснения, за которым происходит довытеснение нефти. Часть воды на фронте вытеснения успевает капиллярно пропитываться, поэтому перед фронтом вытеснения формируется небольшая распыленная область.

Принято считать, что фазовая проницаемость по воде зависит только от текущей водонасыщенности,

$k_{rw}=f(S_w)$

потому при совместной трехфазной фильтрации нефти, воде все равно какого состава углеводородную продукцию вытеснять, для неё они все углеводороды. Эта условность помогает при обработке лабораторных точек по воде, искать зависимость поведения кривой фазовой проницаемости по воде не обращая внимания на количество газа и нефти.

Также считается, что фазовая проницаемость по газу зависит только от текущей газонасыщенности,

$k_{rg}=f(S_g)$

потому подвижность газа зависит от объема пор суммарно занятого жидкостью, будто то нефть или вода. Схожим образом, при построении зависимости кривой фазовой проницаемости по газу можно не обращать внимания в каком соотношении распределена вода и нефть в керне.

Фазовой проницаемости по нефти не повезло. Скорость фильтрации нефти зависит от текущей водо- и газонасыщенности,

$k_{ro}=f(S_w, S_g)$

поэтому подвижность нефти чутко реагирует на выделение газа из нефти и при обработке лабораторных данных нельзя просто собрать зависимости Kro от So, потому как для разных пропорций газа и воды в образце форма кривой фазовой проницаемости по нефти будет своя.

Перейдем к выводу уравнения Баклея-Леверетта (BL) .

Рассматривая элементарный объем пласта и пренебрегая влиянием капиллярных сил и сжимаемостью, можно отметить, что изменение массового расхода нефти вызвано изменением нефтенасыщенности,

$-\frac{\partial}{\partial x}(\rho_o u_o) = \frac{\partial}{\partial t}(\rho_o S_o \phi)$

Для воды также можно записать схожее выражение,

$-\frac{\partial}{\partial x}(\rho_w u_w) = \frac{\partial}{\partial t}(\rho_w S_w \phi)$

Записанные уравнения подразумевают, что нефть не растворима в воде и изменение насыщенности связано только с вытеснением нефти из породы.

Умножая обе части уравнения на площадь фильтрации «A», перейдем от скорости фильтрации к дебиту,

$-\frac{\partial}{\partial x}(\rho_o q_o) = A \cdot \frac{\partial}{\partial t}(\rho_o S_o \phi)$

$-\frac{\partial}{\partial x}(\rho_w q_w) = A \cdot \frac{\partial}{\partial t}(\rho_w S_w \phi)$

В этой простой модели нефть и вода считается несжимаемыми, поэтому плотность принимается постоянной. Пористость также принимается постоянной, что позволяет упростить уравнения до следующего вида,

$-\frac{\partial q_o}{\partial x} = A \cdot \phi \, \frac{\partial S_o}{\partial t}\$

$-\frac{\partial q_w}{\partial x} = A \cdot \phi \, \frac{\partial S_w}{\partial t}$

Нам понадобится отношение доли нефти и доли воды (обводненность) в общем потоке водонефтяной смеси,

$f_o=\frac{q_o}{q_t} =\frac{q_o}{q_o+q_w}$

$f_w=\frac{q_w}{q_t} =\frac{q_w}{q_o+q_w}$

где суммарный дебит нефти и воды, это

$q_t=q_o+q_w$

В современном инженерном языке не прижилось устойчивого выражения для обозначения «доли в потоке», поэтому используется тяжеловесная калька с английского языка «фракционный поток».

Очевидно, что сумма долей равна единице,

$f_o+f_w=1$

поэтому далее можно не рассматривать отдельно уравнение для нефти, а ограничиться только одним уравнением для воды, которое перепишем через обводненность,

$-\frac{\partial f_w}{\partial x} = \frac{A \cdot \phi}{q_t} \, \frac{\partial S_w}{\partial t}$

Из полученного выражения (опуская вывод) получается собственно уравнение Баклея-Леверетта,

$\left ( \frac{dx}{dt}\right )_{S_w} = \frac{q_t}{A \cdot \phi} \, \left (\frac{\partial f_w}{\partial S_w} \right )_t$

Скорость с которой перемещается значение $S_w$ зависит от значения производной обводненности для этой водонасыщенности

$v(S_w) = \frac{q_t}{A \cdot \phi} \cdot {f_w}'$

Можно заметить, что следующий комплекс в уравнении BL является средней реальной скоростью фильтрации,

$v = \frac{q_t}{A \cdot \phi}$

Следовательно, значение производной обводненности показывает на сколько быстрее заданная водонасыщенность перемещается относительно средней скорости фильтрации,

$v(S_w) = v \cdot {f_w}'$

Зная скорость, с которой перемещается заданная насыщенность, не сложно найти и пройденное расстояние.

$x(S_w) = v(S_w) \cdot t$

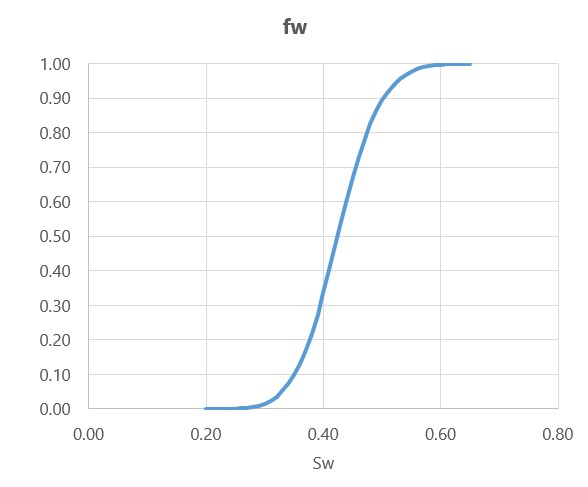
Решение BL позволяет построить распределение изменения насыщенности во времени. Сначала из исходных кривых относительных фазовых проницаемостей рассчитывается кривая доли воды в потоке,

$f_w = \frac{1}{\displaystyle 1+\left ( \frac{k^*_o}{k^*_w}\right )\left ( \frac{\mu_w}{\mu_o}\right )}$

ОФП часто удобно описать одной из аппроксимирующий функцией (Corey, LET) и определить производную в каждой точке водонасыщенности,

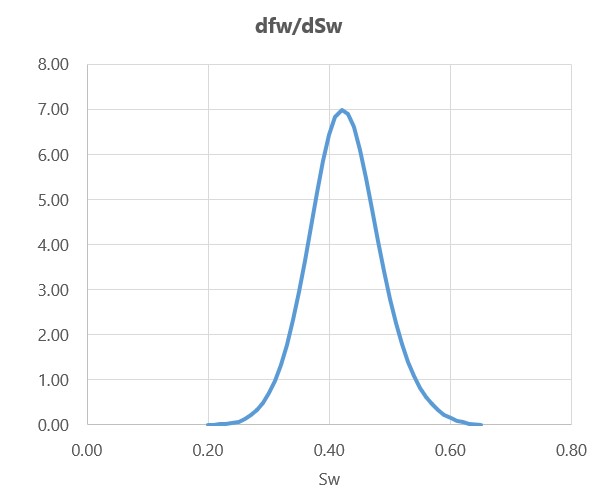
Зная профиль распределения скорости относительно средней скорости фильтрации, построим положение фронта вытеснения, через некоторое время после начала вытеснения,

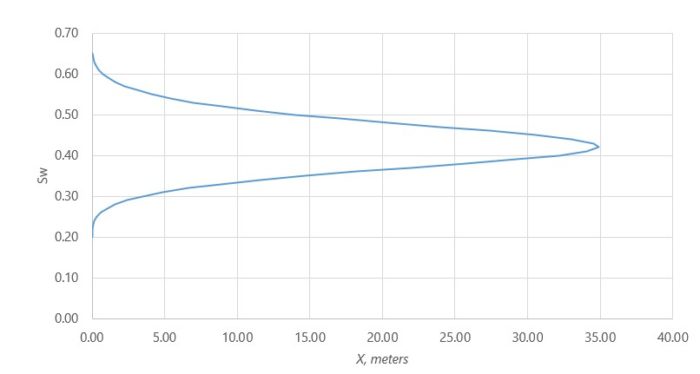
Что не так с этим графиком?

Обращает внимание физически невозможная ситуация наличие двух значений водонасыщенности на одном пройденном расстоянии. Значение водонасыщенности в точке обязательно будет единственным числом.

Разрешение неоднозначности следует из простого наблюдения за процессом вытеснения. Рассмотрим прохождение границы фронта вытеснения на два близких момента времени,

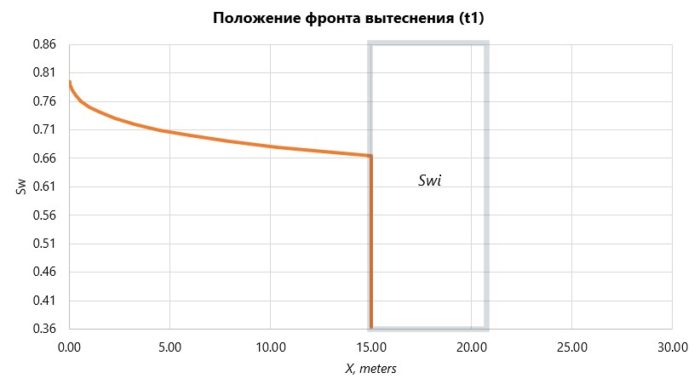
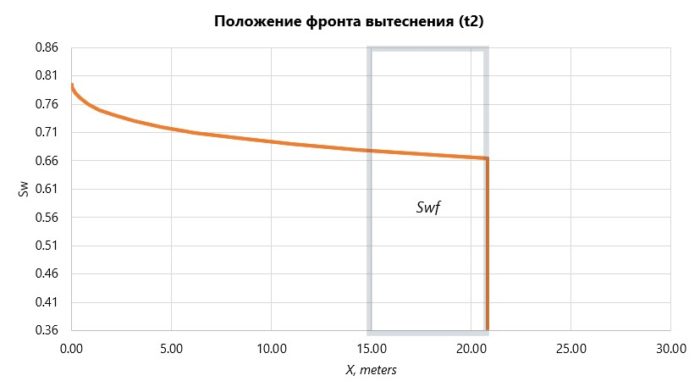
В рассматриваемом объеме пласта за время $(t_2-t_1)$ , водонасыщенность вырастет от начальной $S_{wi} = 0.36$ до некоторого нового значения, которое при уменьшении размера рассматриваемого участка, приближается к значению на фронте вытеснения $S_{wf}$ ,

$\Delta S_w=S_{wf}-S_{wi}$

Через изменение водонасыщенности определим объем воды, который накопится в объеме пласта,

$\Delta V_w=A \phi \Delta S_w \Delta x$

С другой стороны, объем воды можно определить через дебит воды, который поступает в рассматриваемый объем за промежуток времени

$\Delta V_w=q_w \cdot \Delta t=q_t \cdot f_{wf} \cdot \Delta t$

Приравняв объемы воды, получим связь между изменением водонасыщенности и временем

$q_t \cdot f_{wf} \cdot \Delta t = A \cdot \phi \Delta S_w \Delta x$

Определим, какой же величины будет значение обводненности на фронте вытеснения чтобы добиться скачка в насыщении

$f_{wf} = \frac{A \cdot \phi}{q_t} \cdot \frac{\Delta x}{\Delta t} \cdot \Delta S_w$

Совершая предельный переход, получим выражение связывающее значение обводненности на фронте вытеснения и насыщенностью на фронте,

$f_{wf} = {f_w}' \cdot (S_{wf}-S_{wi})$

Записанное выражение графически является касательной из точки Swi к графику функции fw, где точка касания определяет баланс между значением насыщенности на фронте вытеснения и обводненностью.

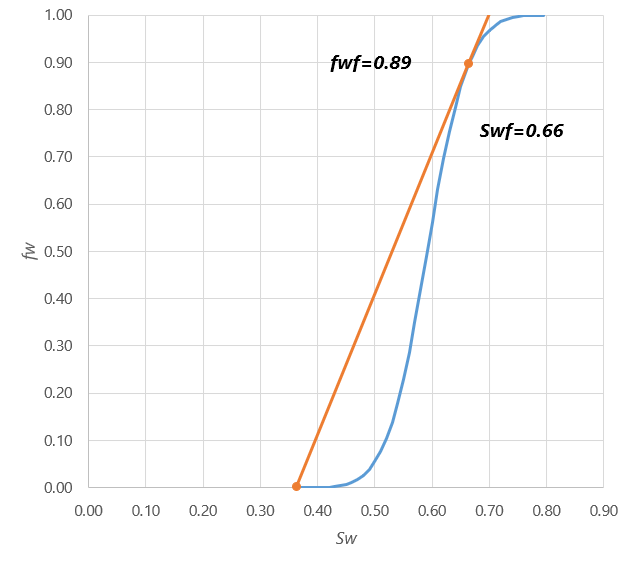
Полученное значение насыщенности определяет максимальную скорость вытеснения нефти водой, значения скорости выше скорости фильтрации фронта вытеснения нефизичны. Это позволит преобразовать ранее показанный профиль скоростей, ограничив скоростной максимум,

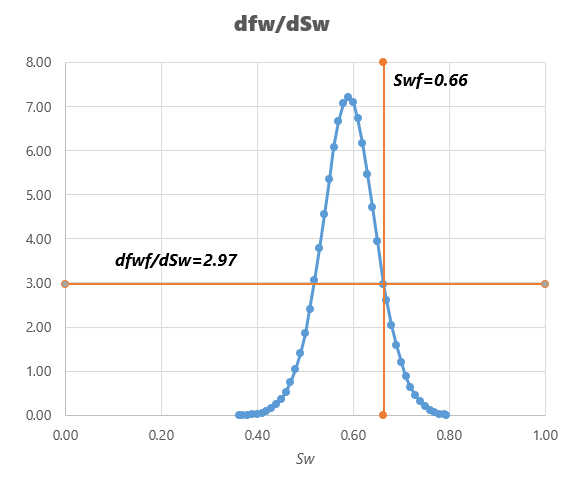
Значение dfwf/dSwf = 2.97 показывает, что фронт вытеснения движется почти в 3 раза быстрее чем средняя скорость фильтрации. Значения множителя скоростей от 3 и выше недостижимы.

В итоге от всей истории, остается только нижний правый квадрат несущий информацию. Значения обводненности от $S_{wf}$ до $S_{wi}$ равны нулю, следовательно в добывающей скважине обводненность меняется скачком и не существует переходной обводненности от $fw = 0$ до $f_w = f_{wf}$ .

Получив правильный профиль скоростей, можно построить распределение насыщенности на разные моменты времени,

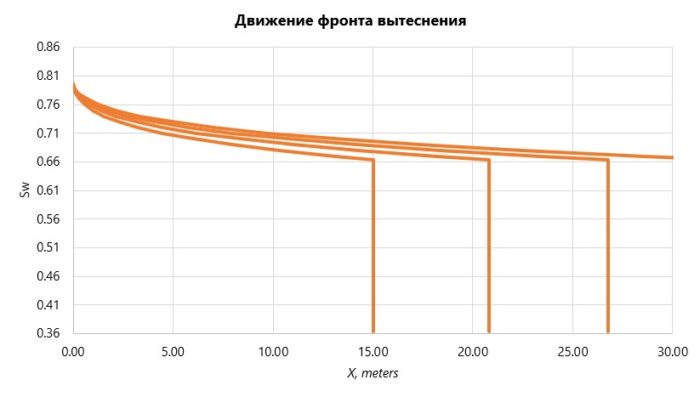
Типичная картина распределения водонасыщенности, полученная в лаборатории экспериментально подтверждает правильность теории BL.

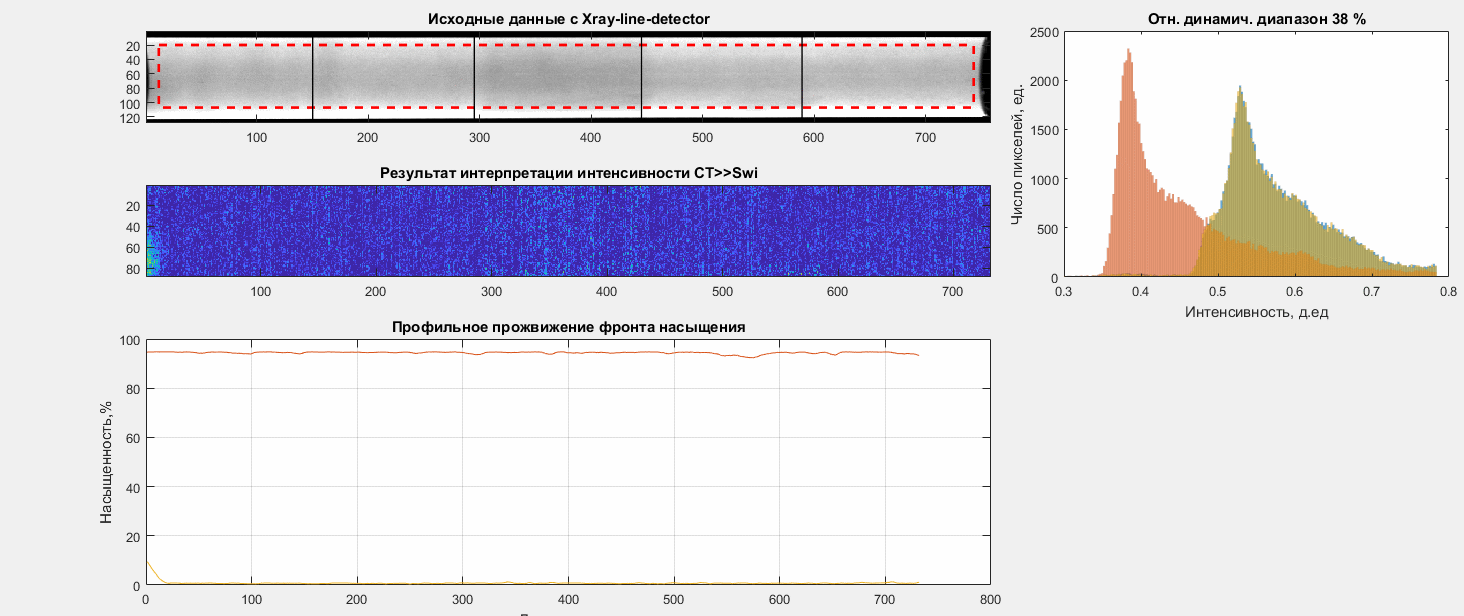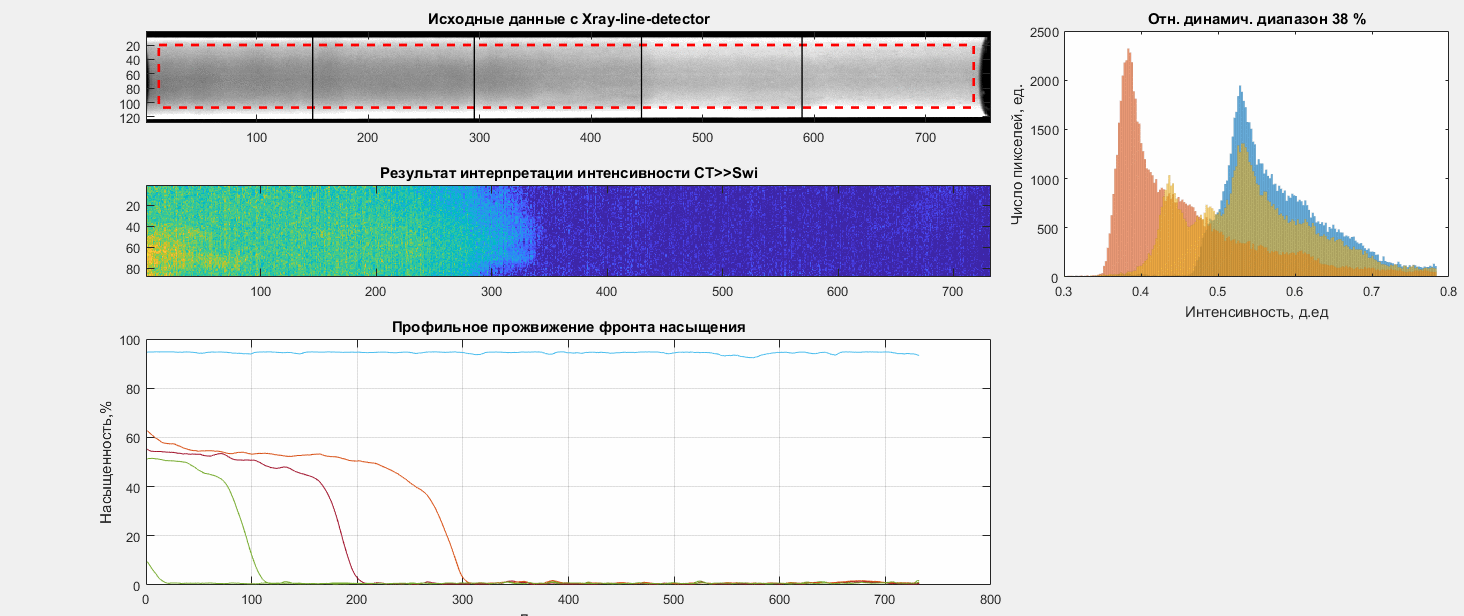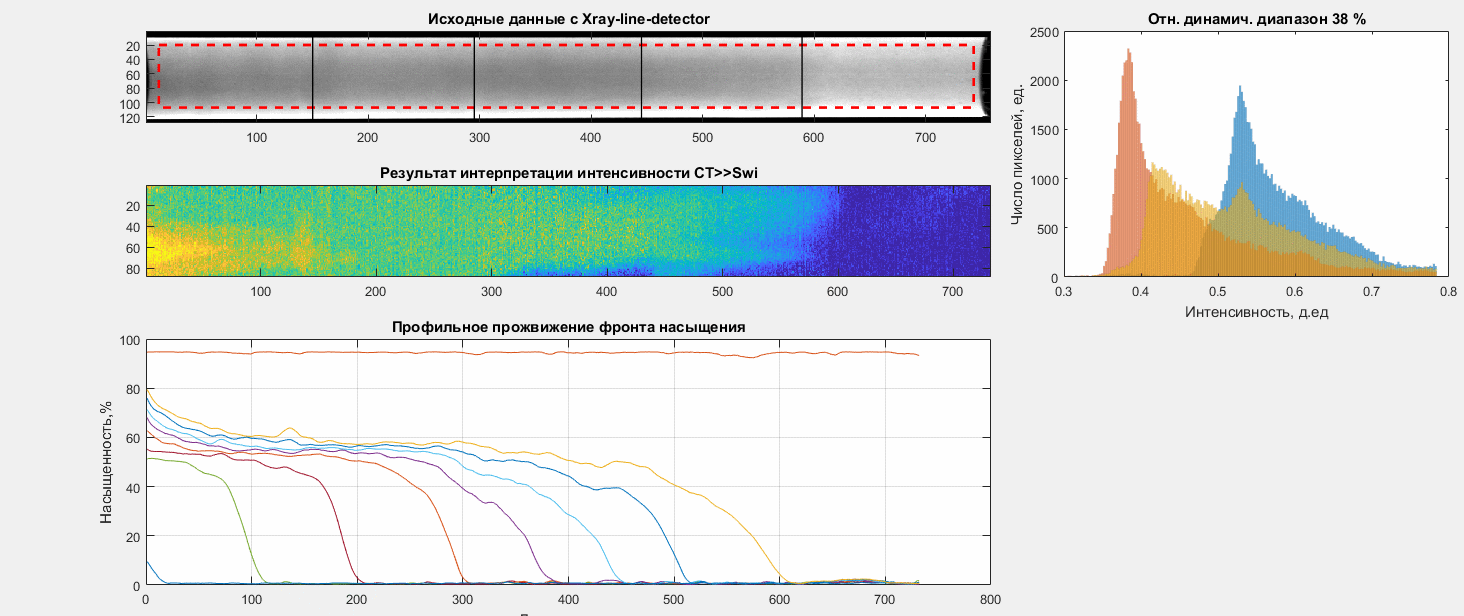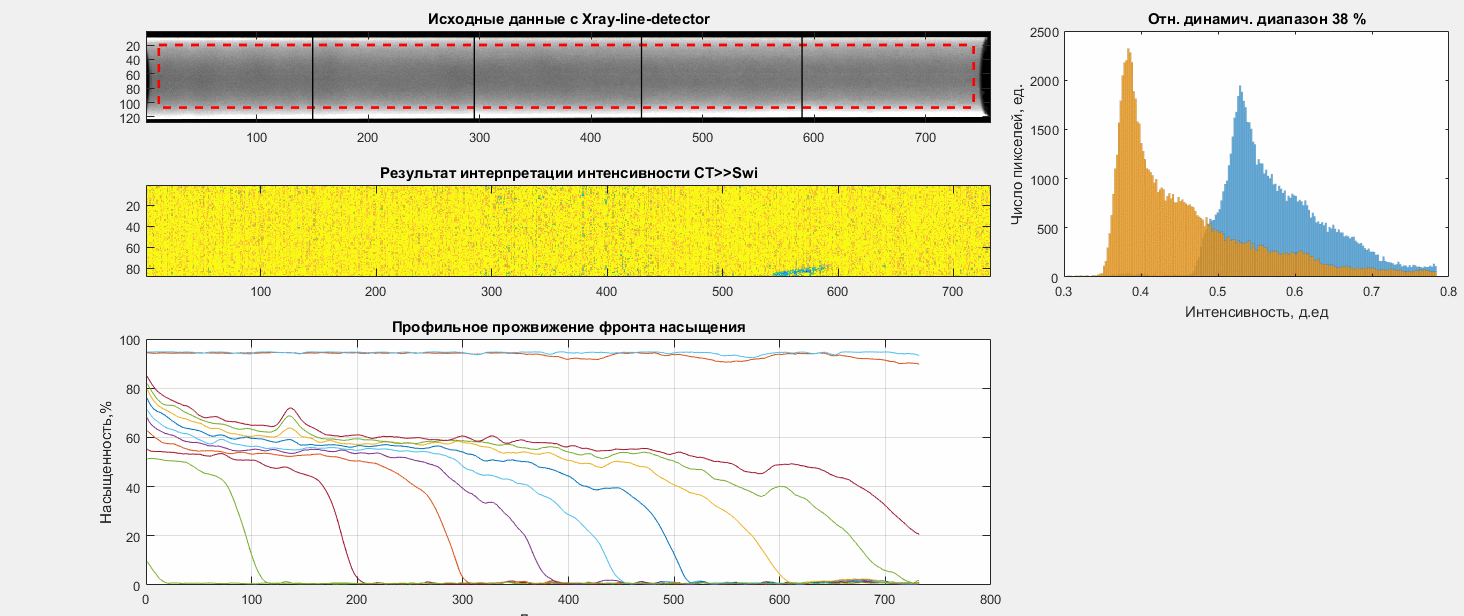
Однако существует некоторые отличия характерные для образцов керна.

На фронте вытеснения за счет капиллярного впитывания некоторое количество воды формирует «стабилизированную зону» $x^*$ , размер которой сохраняется приблизительно постоянным и зависит от отношения,

$\pi_1 = \frac{\sigma}{\sqrt{k/m} \cdot \Delta p}$

Для масштабов месторождения, размер стабилизированной зоны $x^*$ по отношению к расстоянию между скважинами $L$ является малой величиной и не оказывает влияния на динамику обводнения. Однако при лабораторном изучении вытеснения нефти водой, стабилизированная зона может быть сопоставима с длиной образца.

При проведении эксперимента, вода из «стабилизированной зоны» быстрее появится на выходе образца нарушая как величину насыщенности на фронте вытеснения, так и значение обводненности на фронте, поэтому величину $x^*/L$ пытаются уменьшить используя высокие скорости вытеснения, тем самым уменьшая величину критерия $\pi_1$ .

Однако повышение скорости вытеснения, приводит к увеличению градиента давления и изменяет второй критерий подобия — перепад давления необходимый для создания высокой скорости фильтрации может быть намного больше подобного перепада давления в пласте.

$\pi_2 = \frac{\sigma}{k \cdot grad \, p}$

Повышение перепада давления позволяет преодолеть капиллярные силы, которые удерживают остаточную нефть в образце керна и получить искажённую картину процесса вытеснения, завышая величину нефтеотдачи.

Точное выполнение критериев подобия $\pi_1$ и $\pi_2$ возможно было бы при выполнении следующего условия,

$\left [\frac{L^2}{k} \right ]_{core}=\left [\frac{L^2}{k} \right ]_{nature}$

согласно которому, уменьшение линейных размеров при переходе от масштаба месторождения к масштабу керна должно сопровождаться уменьшением и проницаемости образца. С практической точки зрения, подобное кратное уменьшение проницаемости нарушает геометрическое подобие внутреннего порового пространства.

Обычно эксперимент стараются проводить при высокой скорости фильтрации, так чтобы перепад давления был заведомо больше перепада капиллярного давления,

$\Delta p >> p_c$

Величина максимального перепада давления ограничивается ОСТ 39-235-89, где указано и вполне объяснимо почему, что скорость фильтрации выбирается исходя из ожидаемых скоростей фильтрации при разработке изучаемого объекта. Опять же для низкопроницаемых коллекторов пытаясь сохранить низкие скорости фильтрации используют малые перепады давления. В таком случае перепад давления становится сопоставим с капиллярным давлением и часто становится недостаточным чтобы преодолеть капиллярность — вычисленные значения проницаемости фаз становятся очень низкими, не соответствующие добывающим характеристикам скважин.

В целом невозможность соблюдения критерия подобия при переходе от масштаба месторождения к масштабу керна позволяет имитировать разработку месторождения в малом масштабе керна достаточно условно.

§2 Unsteady State Test или Метод вытеснения

Итак, попробуем поставить эксперимент, позволяющий получить зависимости ОФП. Будем нагнетать в нефтенасыщенный образец керна известный объем воды и замерять изменение насыщения в сечениях керна. Из образца начнет вытеснятся чистая нефть, затем через некоторое время нагнетаемая вода появится на выходе образца.

При проведении эксперимента, регистрируются во времени расход нагнетаемой воды, объем вытесненной нефти и воды и перепад давления на образце,

Обработка эксперимента осложняется тем, что построения ОФП требуется определить величину насыщенности на бесконечно малом участке на выходе образца. Для теоретического расчета насыщения используется например графический метод Jones S.C, как это упоминает Добрынин В.М (1988). Несмотря даже на особенности критериев подобия и сложность в обработке, при эксперименте охватывается не весь диапазон насыщенности, а только его часть после прорыва воды. В целом кривые ОФП полученные «методом вытеснения» считаются ненадежными. Главным достоинством эксперимента является скорость.

§3 Steady State Test или Метод стационарной фильтрации

Для образца керна переменная насыщенность воды по длине создает серьезные трудности по обратному расчёту фазовых проницаемостей. К моему удивлению, существует весьма простое решение — это создать постоянную насыщенность по всей длине керна.

Выдержать постоянную водонасыщенность в каждом сечении образца возможно только при сохранении постоянной скорости фильтрации нефти и воды, или другими словами, значений фазовой проницаемости нефти и воды. При проведении эксперимента, в образец подается смесь нефти и воды заданной пропорции до достижения стабилизации водонасыщенности, что сопровождается значительными затратами времени.

Далее, проводится обработка результатов эксперимента.

По известным объемам подаваемой нефти и воды и зная перепад давления, несложно вычислить значения фазовой проницаемости каждой фазы,

$k_{w}=\frac{q_w \cdot \mu_w \cdot L}{A \cdot \Delta p}$

$k_{o}=\frac{q_o \cdot \mu_o \cdot L}{A \cdot \Delta p}$

И значение относительной фазовой проницаемости,

$k_{rw}=\frac{k_w}{k}$

$k_{ro}=\frac{k_o}{k}$

Сравнение распределения водонасыщенности, полученное расчётным путем из ОФП определенных в стационарном эксперименте с экспериментальной водонасыщенностью при вытеснении нефти водой, показывает удовлетворительное согласование друг с другом.

Таким образом, стационарные относительные фазовые проницаемости могут служить надежной основой гидродинамических расчётов, не смотря на то, что они получены не при вытеснении нефти водой.

При проведении исследования наблюдается также капиллярный концевой эффект.

Совместная подача нефти и воды на вход в образец, сопровождается формированием собственного распределения давления в каждой фазе. Разница между давлениями в нефти и воде, называется капиллярным давлением и зависит от текущей водонасыщенности в сечении образца.

Так как насыщенность по образцу не меняется, разница между давлениями сохраняется постоянной. Однако, на выходе из образца давление в фазах нефть и вода сравнивается, что приводит к изменению насыщенности. Это явление называется капиллярным концевым эффектом,

Для устранения влияния концевого эффекта, используется составная модель, где измерение перепада давления и насыщения производится только по центральному образцу.

При подготовки заметки в части теоретического вывода уравнения полностью использовалась книга «Waterflooding» G.Paul Willhite (1986) и статья «Numerical Simulation of the Buckley-Leverette Problem» (2013), где объясняется построение графического решения. Часть материала взял из неизданной книги «Fundamentals of Fluid Flow in Porous Media» материалы которой доступны на сайте лаборатории Perm INC. Обработка экспериментальных данных описана у Добрынина «Фазовые проницаемости коллекторов нефти и газа», про критерии подобия прочитал у Эфроса «Исследования фильтрации неоднородных систем» (1963).

Практическое моделирование

Добавить комментарий Отменить ответ

Archives