Аппроксимация зависимости смоченного угла от объемной доли жидкости

Геометрическое отношение $\theta$ от $R_f$ имеет вид,

$R_f=\frac{\theta - \sin \theta}{2 \pi}$

из которого, нельзя выразить $\theta$ , поэтому приходится использовать численный подбор значений.

В 1999 году выходит статья «An Explicit Approximation for Two-Phase Stratified the Wetted Angle in Pipe Flow» от Dan Biberg.

Численное решение приведенного уравнения может серьезно замедлить расчет многофазного симулятора потока, поэтому существует потребность в более простом решении. При значении $R_f$ близком к нулю, выражение заменим степенным рядом для синуса,

$R_f = \frac{1}{\pi}\left[\delta - \frac{1}{2}(2 \delta - \frac{(2\delta)^3}{6}+...)\right]$

где

$\delta = \frac{\theta}{2}$

Обращая внимание, что при $R_f$ близком к нулю, величина смоченного угла также является малым значением, следующими членами ряда начиная с $\delta^5$ можно пренебречь и выразить угол через объемную долю,

$\delta \approx \left (\frac{3 \pi R_f}{2} \right)^{1/3} \, , R_f \rightarrow 0$

Аналогично, раскладывая в ряд синус при значении $\delta = \pi$ , получим

$R_f = \frac{1}{\pi}\left[\delta - \frac{1}{2}(-2 (\pi - \delta) + \frac{2(\pi - \delta)^3}{6}-...)\right]$

Также обращая внимание, что $\delta$ близка к $\pi$ при стремлении $R_f$ к единице, отбросим члены ряда начиная с 5 степени,

$\delta \approx \pi - \left (\frac{3 \pi (1-R_f)}{2} \right)^{1/3} \, , R_f \rightarrow 1$

Предположим, что решение для произвольного значения $R_f$ в физическом диапазоне $[0..1]$ заключено между этими двумя крайними значениями и искомая функция имеет следующие члены,

$\pi - \left (\frac{3 \pi (1-R_f)}{2} \right)^{1/3} + \left (\frac{3 \pi R_f}{2} \right)^{1/3}$

Ошибка определения значения смоченного угла, в таком случае это разница между истинным значением и искомой функцией,

$E(R_f)=\delta(R_f)- \left [\pi + \left(\frac{3 \pi}{2}\right)^{1/3} \left (R_f^{1/3} - (1-R_f)^{1/3} \right) \right]$

Приближенная апроксимация ошибки определения,

$E(R_f) \approx a_0 + a_1 R_f + a_2 (R_f)^2$

позволяет построить параболу через известные пары значений для пустой, наполовину полной и полной трубы

$(0, 0), (0.5, \pi / 2), (1, \pi)$

Итоговая аппроксимация выглядит следующим образом,

$\delta(R_f) = \pi R_f + \left(\frac{3 \pi}{2}\right)^{1/3} \left (1 - 2 R_f + R_f^{1/3} - (1-R_f)^{1/3} \right) +\epsilon_1$

Для всего диапазона значений ошибка определения угла смачивания составляет $\epsilon_1\pm 0.002$ rad.

Сравнение с прошлой задачей расчета slug режима, представленная апроксимация действительно сокращает вычислительные затраты и позволяет избежать внутренней итерации,

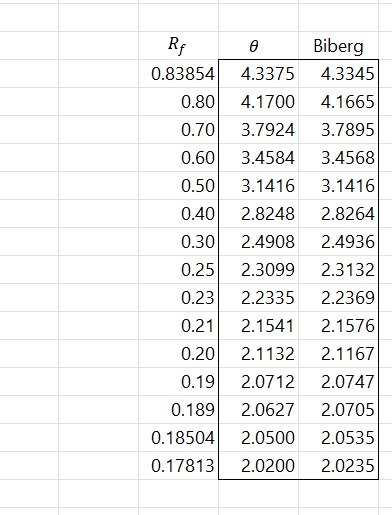
В таком виде, зависимость смоченного угла от объемной доли жидкости используется в симуляторе OLGA.

Практическое моделирование

Аппроксимация зависимости смоченного угла от объемной доли жидкости

Добавить комментарий Отменить ответ

Комментарии

Архивы