Расчет показателей работы скважины BL
В книге «Waterflooding» (1986), в приложении А приведен листинг программы на FORTRAN66, однако мне показалось, что можно переписать проще. В книге также приведен пример расчета, который использовался для контроля правильности написания.
Переписанный код на C# githib
Относительные фазовые проницаемости, описаны функцией Кори
![]()
![]()
public double GetKro(double Swd)
{
return a1 * Math.Pow((1 - Swd), m);
}
public double GetKrw(double Swd)
{
return a2 * Math.Pow(Swd, n);
}
где нормирование насыщенности проводится в интервале от начальной до остаточной нефтенасыщенности,
![]()
public double GetSwd(double Sw)
{
return (Sw - Swi) / (1 - Sor - Swi);
}
Доля воды в потоке (обводненность),
![]()
где,
![]()
public double Getfw(double Swd) // Функция fw в точке Swd
{
double A = (a1 * viscw) / (a2 * visco);
return Math.Pow(Swd, n) / (Math.Pow(Swd, n) + A * Math.Pow((1 - Swd), m));
}
Значение производной от обводненности
![]()
public double GetdfwdSw(double Swd) // Производная fw` в точке Swd
{
double A = (a1 * viscw) / (a2 * visco);
return (1 / (1 - Sor - Swi)) * A * (n * Math.Pow(Swd, (n - 1)) * Math.Pow((1 - Swd), m) + m * Math.Pow(Swd, n) * Math.Pow((1 - Swd), (m - 1))) / (Math.Pow((Math.Pow(Swd, n) + A * Math.Pow((1 - Swd), m)), 2));
}
Определение значения насыщенности на фронте вытеснения происходит простым итеративным методом половинного деления.
Зная, что решение находится в интервале нормированной насыщенности от нуля до единицы, задается начальное приближение Swd = 0.5 и строится уравнение касательной к графику функции fw в этой точке. Если насыщенность подобрана верно, то касательная упадет в точку Swd = 0. В зависимости от того, перелетела ли или не долетела касательная, делается вывод об изменении насыщенности на следующей итерации.
public double GetSwf(double Sw)
{
double L = 0;
double R = 1;
double C = 0;
double Swd; // Нормированная насыщенность
double dfwdSw;
double Y = 1;
double eps = 1e-5;
while (Math.Abs(Y) > eps)
{
C = (L + R) * 0.5;
Swd = GetSwd(C);
dfwdSw = GetdfwdSw(Swd);
// Проводим линию касательной к функции fw, если в точке Swi она не пересекает ноль, значит решение пока не найдено
Y = Getfw(Swd) + dfwdSw * (Sw - C);
if (Y < -eps)
{
L = C;
}
if (Y > +eps)
{
R = C;
}
}
return C;
} // Получить насыщенность на фронте вытеснения
Это всё что касается вспомогательных подпрограмм.
Рассмотрим технологический режим разработки поддержания постоянного перепада давления между нагнетательной и добывающей скважиной. Дебит жидкости в элементарном сечении пласта можно записать как,
![]()
Приведем к привычному уравнению для дебита,
![]()
Запишем в целом для пласта,
![]()
Изменение дебита связано с изменением вязкости жидкости,
![]()
Значение вязкости жидкости в интервале насыщенности от заданной Sw до остаточной нефтенасыщенности, находится интегрированием методом трапеции.
public double GetLaAverage(double Sw) // Определение средней вязкости в интревале насыщенности от Sw до (1 - Sor)
{
// Решение интеграла методом трапеции
int N = 49;
double dSw = (1 - Sor - Sw) / N;
double Swd;
double Kro, Krw;
double La1, La2;
double dfwdSw1, dfwdSw2;
double dfwdSwi;
double LaSum;
double h;
Swd = GetSwd(Sw);
Kro = GetKro(Swd);
Krw = GetKrw(Swd);
La1 = 1 / (Kro / visco + Krw / viscw);
if (dSw == 0) return La1;
dfwdSw1 = GetdfwdSw(Swd);
dfwdSwi = dfwdSw1;
LaSum = 0;
for (int i = 0; i < (N); ++i)
{
Sw = Sw + dSw;
if (Sw > (1 - Sor)) Sw = 1 - Sor;
Swd = GetSwd(Sw);
Kro = GetKro(Swd);
Krw = GetKrw(Swd);
La2 = 1 / (Kro / visco + Krw / viscw);
dfwdSw2 = GetdfwdSw(Swd);
h = dfwdSw1 - dfwdSw2;
LaSum = LaSum + 0.5 * (La1 + La2) * h;
La1 = La2;
dfwdSw1 = dfwdSw2;
}
return LaSum / dfwdSwi;
}
}
На первом этапе расчета, фронт вытеснения нагнетаемой воды не достиг добывающей скважины. Наблюдается период безводной добычи нефти.
Дебит жидкости изменяется обратно пропорционально вязкости системы, по мере прохождения фронта вытеснения,
![]()
Вязкость жидкости в заводненной части остается постоянной и определяется нахождением вязкости от насыщенности на фронте вытеснения Swf до значения остаточной нефтенасыщенности (1-Sor).
В примере используются значения,
![]()
Для заданных параметров Кори, насыщенность на фронте вытеснения,
![]()
И вязкость жидкости,
![]()
Сравнивая полученную вязкость с вязкостью воды, можно отметить, кажущейся вязкость нагнетаемой воды в более чем 3.2 раза выше вязкости воды.
В советской литературе (Борисов Ю.П), использовалось понятие коэффициент увеличения фильтрационных сопротивлений, который показывал, во сколько раз возрастает сопротивление в зоне замещения нефти водой.
![]()
![]()
где
![]()
Определив который, можно рассчитать и среднюю вязкость,
![]()
Подстановка значений в формулу дает такое же значение вязкости 3.2.
Коэффициент безводной нефтеотдачи или же доля отбора нефти из пласта до начала обводнения от порового объема,
![Rendered by QuickLaTeX.com \[ Q_{ibt}=\frac{1}{\displaystyle \left (\frac{\partial f_w}{\partial S_{wf}} \right )} \]](http://oilsim.ru/wp-content/ql-cache/quicklatex.com-75aef0a61d33d59ace7d707804fa986b_l3.png)
Вязкость системы будет линейно изменятся от вязкости нефти в начальный момент времени, до вязкости жидкости в заводненной части в момент прорыва воды,
![]()
В тексте программы безводный период делится на 10 равных частей, для каждой расчетной точки определяется дебит жидкости, который равен дебиту нефти, накопленная добыча нефти в процентах от порового объема и накопленная добыча нефти.
Последняя неопределенная величина, это время.
В каждой расчетной точке нам известен мгновенный дебит жидкости и накопленные добычи жидкости. Сначала определим средний дебит жидкости за период времени,
![]()
Затем добычу жидкости за рассмотренный период времени,
![]()
где поровый объем обозначен как,
![]()
накопленная закачка воды, выраженная в поровых объемах записана через отношение,
![]()
Время которое проходит при переходе от одной расчетной точки к другой,
![]()
Далее просто накапливаем время,
![]()
Собственно, всё готово для расчета показателей разработки в безводный период.
double Qibt = 1 / BL.GetdfwdSw(BL.GetSwd(Swf));
double dQibt = Qibt / 10;
double Labt = BL.GetLaAverage(Swf);
double time = 0;
double Qi_t_prev = 0;
double qt_t_prev = 0;
double qw = 0;
double qo = 0;
double WCT = 0;
for (int J = 0; J <= 10; ++J) // Десять расчетных шагов до начала обводнения
{
double Qi_t = dQibt * J;
double La_t = BL.visco + (Labt - BL.visco) * J / 10;
double qt_t = BL.GetLiquidRate(La_t);
if (J > 0)
{
time = time + 2 * (Qi_t - Qi_t_prev) * 160285 / (qt_t + qt_t_prev); // PV = 160285
}
qo = qt_t;
if (J == 10) // Прорыв в добывающую скважину
{
var fw = BL.Getfw(BL.GetSwd(Swf));
qw = qt_t * fw;
qo = qt_t - qw;
WCT = fw;
}
Qi_t_prev = Qi_t;
qt_t_prev = qt_t;
}
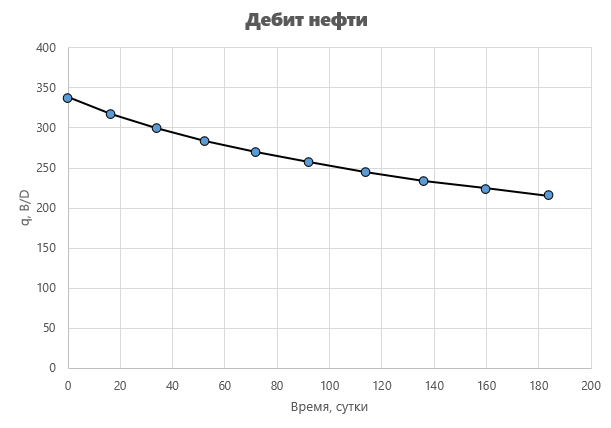
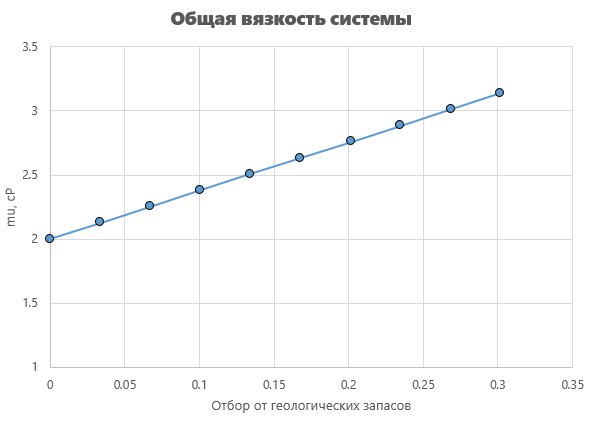
Прорыв фронта вытеснения происходит при отборе 30.2% от запасов нефти.
Второй этап расчета, это период обводнения, когда в добываемой продукции обводненность постоянно возрастает по мере отбора запасов нефти.
Обводненность продукции зависит от значения насыщенности в прискважинной зоне. В момент прорыва фронта вытеснения в скважину, обводненность определяется насыщенностью на фронте вытеснения. Для условий нашего примера, это значение
![]()
Таким образом, обводненность изменяется мгновенно от 0% до 89.6%. В дальнейшем водонасыщенность продолжит расти, до достижения значения остаточной нефтенасыщенности. Для расчета интервал изменения нефтенасыщенности делится на 50 равных частей.
Накопленная добыча нефти, в поровых объемах определяется для каждой точки насыщенности на фронте вытеснения,
![Rendered by QuickLaTeX.com \[ Q_i=\frac{1}{\displaystyle \left (\frac{\partial f_w}{\partial S_{w}} \right )} \]](http://oilsim.ru/wp-content/ql-cache/quicklatex.com-d790ee743c297d324e5a6e1bb9fb839d_l3.png)
И вязкость жидкости, определяется в интервале от текущей насыщенности до остаточной нефтенасыщенности.
Это позволяет построить зависимость вязкости системы от накопленной закачки воды, что позволяет определить дебит жидкости. Зная обводненность нетрудно определить и дебит нефти.
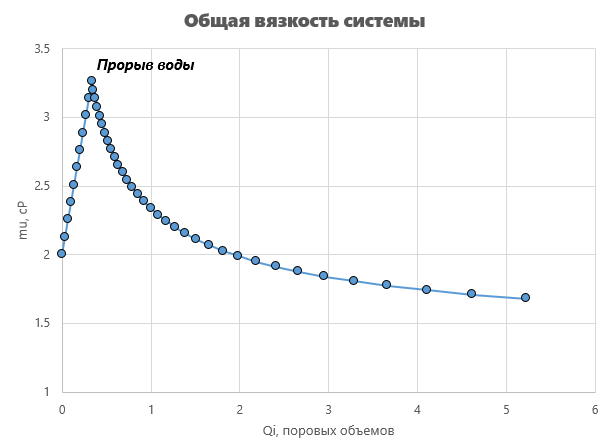
До прорыва воды в добывающую скважину, вязкость системы увеличивалась. Однако после прорыва воды, вязкость начинает снижается и после двух поровых объемов снижается ниже вязкости нефти 2 cP. Таким образом в нашем примере, появление воды в продукции скважины увеличивает продуктивность скважины, что сказывается на росте дебита жидкости.
N = 51;
dSw = (1 - BL.Sor - Swf) / (N - 1);
Sw = Swf;
for (int i = 0; i < N - 2; ++i)
{
Qi = 1 / BL.GetdfwdSw(BL.GetSwd(Sw));
var La = BL.GetLaAverage(Sw);
var qt_t = BL.GetLiquidRate(La);
var fw = BL.Getfw(BL.GetSwd(Sw));
var Swav = Sw + (1 - fw) / BL.GetdfwdSw(BL.GetSwd(Sw));
qw = qt_t * fw;
qo = qt_t - qw;
WCT = fw;
if (WCT > 0.999) break;
if (i > 0)
{
time = time + 2 * (Qi - Qi_t_prev) * 160285 / (qt_t + qt_t_prev);
text.WriteLine($"{time:F1}\t{qo:N2}\t{qw:N2}\t{qt_t:N2}\t{WCT:N3}\t{Qi:N3}\t{Qi:N3}\t{160.285 * (Swav - BL.Swi):N3}\t{La:N4}");
}
Qi_t_prev = Qi;
qt_t_prev = qt_t;
Sw = Sw + dSw;
}
Объединяя показатели для безводного периода и периода после прорыва воды, получим показатели работы скважины.
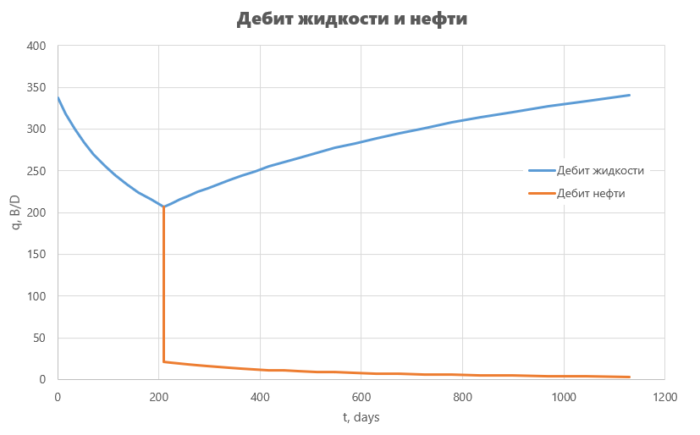
Характеристика вытеснения нефти водой,
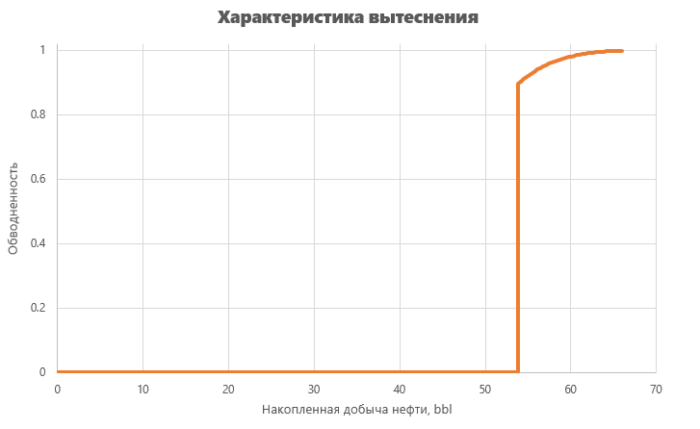
Расчет накопленной добычи нефти производится через изменение средней водонасыщенности в пласте,
![]()
![]()