Flow Pattern Map in Horizontal Pipes (Duckler & Hubbard)

Продолжим изучать статью «A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow» (1976).

Граница между слоистым (S), прерывистым (I) и кольцевым (AD) режимом течения

Обширные экспериментальные и аналитические исследования перехода от слоистого ([S]tratified) к прерывистому течению ([I]ntermittent), проведенные Duckler и Hubbard, показали следующее.

На входе трубы всегда наблюдается слоистое течение. Повышение скорости течения жидкости приводит к повышению уровня жидкости в трубе и формированию волн на поверхности, которые быстро растут стремясь перекрыть сечение трубы. Если скорость течения газа при этом низкая — жидкость образует перемычку. Такой режим течения называется пулевой (slug) либо пробковый (plug).

При дальнейшем повышении скорость течения газа объема жидкости бывает недостаточно для удержания перемычки, а иногда и для образования её. Возникающие волны поднимаются по стенкам трубы, образуя замкнутое кольцо с поверхности которого потоком газа частично уносится капельная жидкость ([A]nnular-[D]ispersed).

Как следует из наблюдений, смена режима течения связана с высотой образующихся волн и переход этот четко выражен.

Рассмотрим случай слоистого течения жидкости с уже образованной волной на поверхности. При увеличении скорости движения газа, давление в газовой фазе снижается за счет эффекта Бернулли, что приводит к дальнейшему росту высоты волн. С другой стороны, сила гравитации стремится погасить волны.

Теория Кельвина — Гельмгольца (Kelvin-Helmholtz) предлагает условие образования волн бесконечно малой высоты, на плоской поверхности жидкости, текущей между двух параллельных пластин.

Согласно теории, волны начинают расти когда, скорость газа превысит критерий стабильности,

$u_g > \sqrt{\frac{g (\rho_l-\rho_g) h_g}{\rho_g}}$

где $h_g$ — расстояние от верхней пластины до поверхности жидкости.

Критерий стабильности можно расширить и на случай волны конечной высоты.
Пусть волна имеет пик высотой $h`$ , толщина газового слоя над волной составляет $h`_g$

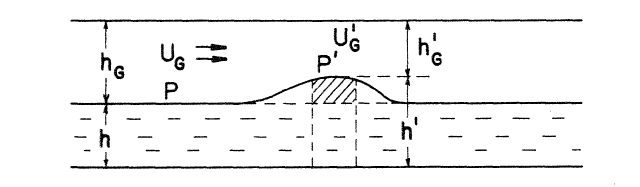
Если пренебречь качанием волны, условие для роста волны можно записать

$P - P` > (h_g - h`_g)(\rho_l - \rho_g) \, g \, \cos \beta$

где перепад давления, за счет сужения потока

$P - P` = \frac{1}{2} \, \rho_g \, (U^{`2}_g-U^2_g)$

Критерий стабильности преобразуется к следующему,

$u_g > \sqrt{\frac{2 (\rho_l-\rho_g) \, g \, (h`-h)}{\rho_g} \cdot \frac{h^{`2}_g}{h^2_g-h^{`2}_g}$

учитывая, что высота волны это

$h`-h = h_g - h`_g$

получим критерий K-H с учетом конечной высоты волны,

$u_g > C_1 \cdot \sqrt{\frac{g \, (\rho_l-\rho_g) \, h_g }{\rho_g}}$

где коэффициент $C_1$ зависит от размеров волны,

$C_1 = \sqrt{\frac{2}{\frac{h_g}{h`_g} (\frac{h_g}{h`_g} + 1)}$

Для бесконечно малого возмущения, отношение высот $h_g/h`_g \rightarrow 1.0$ , что возвращает нас к исходному критерию K-H.

Здесь возникает небольшая нестыковка. Так как коэффициент $C_1$ меньше единицы, при одинаковой скорости газа волны конечной размерности возникнут раньше чем волны бесконечно малого размера. Wallis и Dobson (1973) провели обработку экспериментальных данных и установили, что коэффициент C = 0.5.

Для круглых наклонных труб таким же простым методом можно выразить критерий образования волн с учетом наклона трубы,

$u_g > \sqrt{\frac{2 (\rho_l-\rho_g) \, g \, \cos\beta (h`-h)}{\rho_g} \cdot \frac{A^{`2}_g}{A^2_g-A^{`2}_g}$

где $A_g$ и $A^{`2}_g$ представляют площади сечения газа, соответственно, над невозмущенной пленкой жидкости и над волной.

При малых возмущениях можно разложить $A^`_g$ в ряд Тейлора

$u_g > C_2 \sqrt{\frac{(\rho_l-\rho_g) \, g \cos \beta \, A_g }{\rho_g (dA_l/dh) }$

где значение производной изменения площади сечения занятого жидкостью к высоте уровня,

$\frac{dA_l}{dh} = D \cdot \sqrt{1-\left(\frac{2h_l}{D} - 1\right)^2}$

Коэффициент $C_2$ обращается в единицу, так же как и ранее $C_1$ для бесконечно малого возмущения.

$C_2 = 2 \cdot \frac{(A^`_g/A_g)^2}{1 + A^`_g/A_g} \approx \frac{A^`_g}{A_g}$

Таким образом опять возвращаясь к форме критерия K-H.

Множитель $C_2$ содержит неизвестную площадь сечения газа над волной $A^`_g$ .

Если уровень жидкости близок к верхней точки трубы, площадь занятая газом $A_g$ очень маленькая и любое возмущение на поверхности перекрывает сечение, поэтому коэффициент $C_2$ стремится к нулю. И наоборот, если уровень жидкости незначителен, возникновение волн имеет слабое влияние на площадь занятую газом и поэтому $C_2$ стремится к 1.0.

Предположим, что $C_2$ может быть заменен на более простое выражение,

$C_2 = 1 - \frac{h}{D}$

Граница между гладким слоистым (SS) и волновым слоистым (SW) режимом течения

Переход от гладкого течения к волновому происходит когда скорость газа с одной стороны достаточна для формирования волн, но с другой стороны не достаточна для быстрого роста волны, приводящей к прерывистому или кольцевому режиму течения.

Явление образование волн достаточно сложное и не до конца изучено. Общепринято понимать, что волны возникают когда давление и касательные силы преодолевают вязкостные силы. Однако существуют серьезные разногласия в понимании механизма передачи энергии.

В этой работе используется идеи Jeffreys (1925), который предложил следующий критерий,

$(u_G -c)^2 c > \frac{4 \, \nu_L \, g (\rho_L - \rho_G)}{s \cdot \rho_G}$

s это коэффициент укрытия.

В оригинальной работе Jeffreys принято значение 0.3. Однако, опираясь на экспериментальные исследования Benjamin (1959) получены более низкие значения коэффициента в пределах от 0.01 до 0.03. В этой работе используется значение $s = 0.01$

с это скорость распространения волн.

Для большинства условий формирования волн можно ожидать, что $u_G \gg c$ . Теория посвященная изучению волн предполагает, что отношение скорости распространения волны к средней скорости жидкости $c/u_L$ уменьшается с ростом числа Рейнольдса. Для турбулентного течения жидкости это отношение составляет от 1 до 1.5.

Считая точное положение границы раздела режимов не сильно важным, используется простое отношение

$u_L = c$

Такие предположения дают следующий критерий для границы перехода от слоистого к волновому режиму течения,

$u_G \geq \left[ \frac{4 \, \nu_L \, g (\rho_L - \rho_G) \cos \alpha }{s \cdot \rho_G \cdot u_L} \right ] ^ {1/2}$

Граница между прерывистым (I) и пузырьковым режимом (DB)

При высокой скорости течения жидкости и малой скорости течения газа, происходит смешивание потоков. Сначала газ собирается в виде пузырей, которые при повышении скорости жидкости разбиваются на мелкие распыленные пузыри газа. Предполагается, что переход к такому пузырьковому режиму течения, возникает когда турбулентные флуктуации потока жидкости преодолевают архимедовую силу, за счет которой газ собирается в верхней части сечения горизонтальной трубы.

Сила всплытия пузырька газа,

$F_B = (\rho_L - \rho_G) \, g \, \cos \alpha A_G$